How Fast Does a Sandbag Hit the Scaffolding in a Pulley System?

[mizzy]

Homework Statement

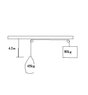
In trying to lift a sandbag B attached to the rope as in the attached figure, a worker at the top of the scaffolding dumps his tools and lunch kit into the box A so that it is now 80kg. if the sandbag is 65kg, find its speed as it hits the scaffolding. Assume that the sandbag starts from rest.

Homework Equations

W=Fd

Win = change in kinetic + change in potential + Wout

The Attempt at a Solution

I started by drawing 2 free body diagrams.

Can someone guide me? Not too sure where to start.

 

[graphene]

This is easily done using energy conservation.

Write down the totl energy (kinetic & potential energy) of the system (both the blocks) at the initial position & the final position.

Then equate the two to find v. (the two blocks & the rope move have the same acceleration & so will have the same speed at any instant)

 

[mizzy]

SO do I use KE + PE = 0?

Do I add the total energies of both objects?? or keep them separate?

 

[Agent M27]

For this problem you want to use the conservation equation as follows:

mgh_i + $$\frac{1}{2}$$mv²_i = mgh_f + $$\frac{1}{2}$$mv²_f

So the equation is more so $$\Delta$$U_g + $$\Delta$$KE=0

As graphene mention being that the objects are connected via the same rope they will have the same velocities. Also if you write down what all your initial and final P.E.'s and K.E.'s it will be easier for you to see how they apply to the above equation. Hope that helps.

Joe

 

[mizzy]

is the inital height 0 and the final height is 4.2?

 

[mizzy]

Ok, i got my answer. I hope I did this right. If I made a mistake, please let me know where I did wrong. Thanks.

I found the total energy for the sandbag and the box.

SANDBAG:
1/2mv2^2 - 1/2mv1^2 + mg(h2 - h1) = 0
1/2(65)v2^2 - 0 + (65)(9.8)(4.2 - 0) = 0
32.5 v2^2 + 2675.4 = 0 (equation 1)

BOX:
1/2mv2^2 - 1/2mv1^2 + mg(h2 - h1) = 0
1/2(80)v2^2 - 0 + (80)(9.8)(0 - 4.2) = 0
40v2^2 - 3292.8 = 0 (equation 2)

I added both equations and came up with this:
72.5v2^2 - 617.4 = 0

solved for v2 --> 2.9m/s

Is that correct?

 

[mizzy]

can someone look over my work and tell me if i did it right? Thanks in advance

 

[Doc Al]

You got the right answer, but only because you added the equations. The separate equations for sandbag and box are not correct. It's only the total mechanical energy of both that is conserved, not the energy of each separately.

Think of it this way: ΔPE_sandbag + ΔPE_box + ΔKE_sandbag + ΔKE_box = 0

But ΔPE_sandbag + ΔKE_sandbag = 0 is not true! Same for the box.

 

[mizzy]

Thanks. Is that true for pulleys, the total mechanical energy of both is conserved??

 

[Doc Al]

Is that true for pulleys, the total mechanical energy of both is conserved??

If you mean like an Atwood's Machine (masses hanging over a pulley), then yes--as long as there's no friction.