hsbc2003
- 5
- 0
Homework Statement
Just need some direction on the problem.
1. Homework Statement
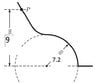
A poorly designed playground slide begins with a straight section and ends with a circular arc. A child starts at point P and slides down both sections of the slide. At some point on the circular arc, the normal force goes to zero and the child loses contact with the ramp. Assuming the forces of friction are negligible, at what height from the ground will the child become airborne.
(( picture in the attachment))
the height from point p to the ground is 9 m. The radius of the arc is 7.2 m.
Homework Equations
w=kf-ki+uf-ui; ki=0, ui=mg(9)
The Attempt at a Solution
well, i figure out the speed in which the particle will be when it hits the circular arc, where uf=mg(7.2). Now how do i figure out how high it will be from the ground when the child will become airborne? I think I need to use F=mv^2/r somewhere in the equation to figure out the force needed for the particle to stay in the circular path and not go flying off. But after that, I'm kind of lost.
Thanks for the help.