oujea
- 11
- 0
Hello
Can someone please explain me how is system
y(t)=dx(t)/dt non-causal and system with memory? I tried it using derivation definition, but I did not understand it.
Also I'm interested in integral of x(T)dT (from -inf to to) - is it always causal and how? Do you have any literature or links where it is well explained.
Thank you in advance
EDIT:
I found this:

and this:
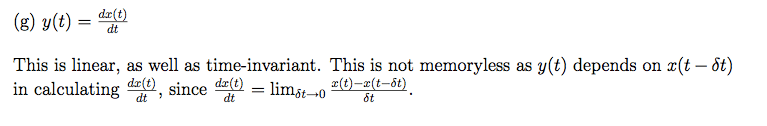
How can I know from this definition of derivative that it is not causal? And on those two pictures, dx(t)/dt definition is different, so what's correct? I have before seen second one, but never the first one.
Can someone please explain me how is system
y(t)=dx(t)/dt non-causal and system with memory? I tried it using derivation definition, but I did not understand it.
Also I'm interested in integral of x(T)dT (from -inf to to) - is it always causal and how? Do you have any literature or links where it is well explained.
Thank you in advance
EDIT:
I found this:
and this:
How can I know from this definition of derivative that it is not causal? And on those two pictures, dx(t)/dt definition is different, so what's correct? I have before seen second one, but never the first one.
Last edited: