mcastillo356
Gold Member
- 658
- 361
- TL;DR
- It computes the supplementary
Exercise statement :
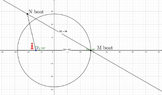
From a lighthouse you can see two boats. Ship ##M## is forty-two kilometers out to sea, and ship ##N## is at an unknown distance. If the distance between the ships is fifty-six kilometers and the angle formed in ##M## is thirty grades, how many kilometers are there from the lighthouse to ##N##, and which is the angle formed in the position of the headlamp?
1) $$b^2=a^2+c^2-2ac\cos{(\theta)}=826.336\Rightarrow{b=\sqrt{826.336}}=28.746$$
2) $$\cfrac{28.74}{\sin{(30^o)}}=\cfrac{56}{\sin{(x)}}\Rightarrow{x=77}$$
As shown at the Geogebra file, the angle is ##103^o##
Also, where is the guiding light at the sketch drawn?
Marcos
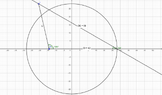
From a lighthouse you can see two boats. Ship ##M## is forty-two kilometers out to sea, and ship ##N## is at an unknown distance. If the distance between the ships is fifty-six kilometers and the angle formed in ##M## is thirty grades, how many kilometers are there from the lighthouse to ##N##, and which is the angle formed in the position of the headlamp?
1) $$b^2=a^2+c^2-2ac\cos{(\theta)}=826.336\Rightarrow{b=\sqrt{826.336}}=28.746$$
2) $$\cfrac{28.74}{\sin{(30^o)}}=\cfrac{56}{\sin{(x)}}\Rightarrow{x=77}$$
As shown at the Geogebra file, the angle is ##103^o##
Also, where is the guiding light at the sketch drawn?

Marcos