How Is the Initial Speed of a Projectile Calculated Using a Ballistic Pendulum?

[yesiammanu]

Homework Statement

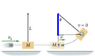
A ballistic pendulum is a common device that is designed to measure the speed of small projectiles. As shown in the sketch on the right, it is composed of an initially stationary metal "cage" which traps the projectile and is suspended vertically by a very light weight rod attached to a low friction pivot. The bottom of the cage is usually equipped with a "pawl" (not shown) which prevents it from slipping backward after reaching it's maximum height. In a particular experiment, the projectile is a steel ball with a mass of 50.0 grams, the cage assembly has a mass of 250. grams, and the length L from the pivot to the center of mass of the entrapped ball + cage = 25.0 cm. After firing, the ball + cage reach a maximum angle from the vertical of 35.0. What was the initial speed 0o of the ball?

Homework Equations

Conservation of Angular Momentum
L = r x p
L = Iw
I = MR² for a thin cylindrical shell
w = v/r
1/2 Iw² = mgh

The Attempt at a Solution

L of ball = r x p = .25m * .05kg * v₀ = .0125m * kg v₀
L of ballistic pendulum + ball = Iw = (.3kg)(.25m)²w = .01875kg * m²w
.0125m * kg v₀ = .01875kg * m²w

v₀ = 1.5m * w
v₀/1.5m = w

1/2 * MR² * v₀²/2.25m² = (.300kg)(9.8 m/s²)(.25m sin35)
1/2 * (.300kg)(.0625 m²)* v₀²/2.25m² = .42 kg* m²/s²
.0041 kg v₀² = .42 kg* m²/s²
v₀² = 102.43 m²/s²
v₀ = 10.1 m/s

The correct answer is 5.65, so I'm not sure where I messed up.

 

[Infinitum]

1/2 * MR² * v₀²/2.25m² = (.300kg)(9.8 m/s2)(.25m sin35)

You applied the conservation of energy here, I believe? So, is the RHS of the equation really the potential energy gained?

Hint: Did the system go up by Rsin\theta?

 

[yesiammanu]

I would think it did, since the height changed and it ends up with 0 speed at 35 degrees

Did I need to factor in kinetic energy since it changes the x position? I thought it would be covered by angular

 

[Infinitum]

I would think it did, since the height changed and it ends up with 0 speed at 35 degrees

Umm, no.

Is the sin projection of the rod really the height gained? (No!) Also, check the cos projection...Is that the height either? What manipulation will give you the height gained by the system?

 

[yesiammanu]

Hmmm.. I'm really confused

I tried to make a construction but I got even more confused

I thought that would just be Lsin35, since if sin was 90 degrees, you would be at exactly L

 

[Infinitum]

Please check attached image. That pink line is not equal to L, nor is the green angle equal to 35⁰.

See the other attachment. What is the length of the blue line in terms of the given data?

 

[yesiammanu]

hmmm...
cos theta = adj/hyp
hyp cos theta = adj
L cos 35 = adj for blue line

And then the red line would be L - Lcos35? so .25m - .25mcos35 = .045m?

 

[Infinitum]

hmmm...
cos theta = adj/hyp
hyp cos theta = adj
L cos 35 = adj for blue line

And then the red line would be L - Lcos35? so .25m - .25mcos35 = .045m?

You got it!

 

[yesiammanu]

Replaced that in my equation and got 5.68, which is probably close enough. Thanks for help!