How Is the Moment of Inertia Calculated for a Wheel Composed of Welded Rods?

[leeone]

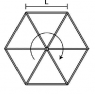
Twelve uniform, thin rods of mass and length are welded
together to form a “wheel” as shown in the figure. What is the
moment of inertia of this wheel for rotation around an axis through
its center and perpendicular to the plane of the wheel? The welds
contribute no mass to the wheel.

I understand the contributions from the spoke...but how would I get the contribution from the six rods around the circumference?

I think it can be done by noting I=1/3ML^2 for a rod with the pivot center at the end and I=1/12ML^2 when the pivot center at the middle.


If i try and integrate the from the center along the circumference I have

I=∫M/L (x^2)dx

but how would I get my limits of integration? I would have to integrate through an angle zero to a fixed distance from the center? SO ((3)^1/2)/2Lcos(Θ)dΘ integrate from 0 to (360)/6=60 degrees, correct?

 

[TSny]

Are you familiar with the parallel axis theorem? If so, can you use it to get I for one of the perimeter rods?

 

[leeone]

That's what my first attempt was...but where would a convenient point be to compute the moment of inertia? If I move along one of the spokes to the outside I feel like I am in the same situation as I was before.

 

[TSny]

That's what my first attempt was...but where would a convenient point be to compute the moment of inertia?

The parallel axis theorem states $I = I_{cm} + Md^2$. What does $d$ represent here?

Can you find $d$ for one of the perimeter rods?

 

[leeone]

would d be (L)root(3)/2...(the vertical distance from the center?)

 

[TSny]

would d be (L)root(3)/2...(the vertical distance from the center?)

Yes!

 

[leeone]

I figured it out! I =(1/12l^2 +3/4L^2 )6 + (1/3Ml^2(6)=7mL^2

Thanks!