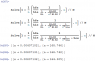How Is the Turn-Ratio n Estimated in a Common-Emitter Oscillator?

[suv79]

Homework Statement

estimate the value of turn-ratio n

[/B]

R1=4.7 kΩ, R2=24 kΩ, Rl=2.7 kΩ, hfe=250, hoe=10^-5, hie=4 kΩ

Homework Equations

loop gain=1/n[hfe/hie*R'l]

R'l=Rl||hoe||[n^2(R1||R2)]

[/B]

The Attempt at a Solution

loop gain=1

[/B]

 

[rude man]

1. Open the feedback loop and calculate the complex voltage gain (amplitude and phase. In doing so, the transformer secondary must be loaded wit the same complex impedance that the closed loop sees.) Assume k=1 for the transformer.
2. Invoke the Barkhausen criterion or whatever it's called these days: O/L gain = 1.0,
phase = 0.

 

[suv79]

yes loop gain is 1 to make it oscillate, and the feedback is positive, so there is no phase shift. :)

iam having a problem with my maths, to work out 'n'
in my attempt i have got stuck

 

[rude man]

yes loop gain is 1 to make it oscillate, and the feedback is positive, so there is no phase shift. :)

iam having a problem with my maths, to work out 'n'
in my attempt i have got stuck

so let's see your math

 

[suv79]

https://www.physicsforums.com/attachments/upload_2014-11-23_23-34-57-png.75772/

its here :)

 

[rude man]

https://www.physicsforums.com/attachments/upload_2014-11-23_23-34-57-png.75772/

its here :)

Stand by, am looking at this some more.

 

[suv79]

ok :) so i can ignore the siemens Hoe, reciprocal which is very large,

i was thinking it was quadrature, :) but was not sure

 

[rude man]

ok :) so i can ignore the siemens Hoe, reciprocal which is very large,

i was thinking it was quadrature, :) but was not sure

Right, h_oe can be ignored.
What do you mean by quadrature? What would shift the phase of h_oe by 90 degrees?
I'm still looking at this. It does look (right now, to me), as though we need to solve an equation of the form
1/nR_L + 1/n³R + 1/n³h_ie = h_fe/h_ie. Maybe Wolfram Alpha can help.
You should not have introduced numbers until the very end.
I'll double-check this some more soon.

 

[suv79]

 

[suv79]

cancel out top and bottom ?

 

[rude man]

cancel out top and bottom ?

You could cross-multiply in the denominator, then cance l out n²(R1 + R2). Tha's assuming your equation is right to begin with.

Looking at your 1st eq'n in post 9, this is a lot like what I have:
change your R'_L into a conductance 1/R'_L:

so 1/R'_L = 1/R_L + 1/ n²R
where I define R = R1||R2.
Now, what I notice is you didn't include h_ie as a load on the transformer secondary. So the above changes to
1/R'_L = 1/R_L + 1/ n²R + 1/n²h_ie
And your 1st equation in post 9, being

(ignore 2nd & 3rd equations)
makes your equation 1 = (1/n)(h_fe/h_ie)/(1/R'_L) with the new 1/R'_L
which wouild then agree with what I came up with.
So, bottom line, include conductance 1/n²h_ie and write the equation in conductances rather than admittances, and you have a cubic expression for n that goes as an³ + bn² + c = 0.

EDIT: I looked up the solution for this equation with b = -1 and it is horrendous. You would definitely need some kind of math software to solve for n. I would leave the equation as is and hand it in with the answer being "the real solution of an³ - n² + c = 0." :) (Defining a and c of course in given parameters).
(The other two solutions are imaginary).

 

[suv79]

i don't think i need 1/n2hie
because equations given in the question don't not have it in for R'L

 

[rude man]

i don't think i need 1/n2hie
because equations given in the question don't not have it in for R'L

h_ie is in parallel with R₁||R₂. You included R₁||R₂; why not also h_ie? And h_ie and R₁||R₂ are almost equal so you can't say h_ie >> R₁||R₂.

 

[suv79]

R'L is effective resistive load, R1||R2 feeds the transformer
hie is the input impedance

 

[rude man]

You can make a tentative assumption that n >> 1 and solve for n. This makes the math trivially simple. Then, if it turns out that n >> 1 you were justified in the assumption.

 

[The Electrician]

Now, what I notice is you didn't include h_ie as a load on the transformer secondary. So the above changes to
1/R'_L = 1/R_L + 1/ n²R + 1/n²h_ie

It looks to me like neglecting h_oe makes a much larger difference than neglecting the loading effect of h_ie

 

[rude man]

Your values for n correspond very well with mine ( n = 164 to 169 range; I came up with n = 169. As I said, you can make life much simpler if you assume n >> 1, then all you're left with is R'_L = R_L.