_N3WTON_
- 350
- 3
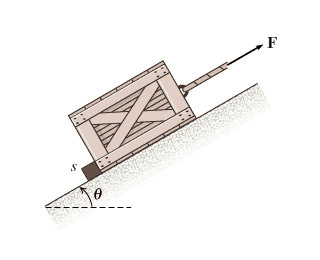
A stop block, s, prevents a crate from sliding down a \theta = 33 \hspace{2 mm} degrees incline. A tensile force F = (F_{o}t) N acts on the crate parallel to the incline, where F_{o} = 325 \frac{N}{s}. If the coefficients of static and kinetic friction between the crate and the incline are \mu_{s} = 0.325 and \mu_{k} = 0.225, respectively, and the crate has mass of m = 50.8 kg, how long will it take until the crate reaches a velocity of v = 2.44 \frac{m}{s} as it moves up the incline.
I know when f < f_{max} = \mu_{s}mgcos(\theta), the system isn't moving, and the net force is:
F - mgsin(\theta) - f = 0.
f = F-mgsin(\theta) < \mu_{s}mgcos(\theta)
When t = t_{1}, f = \mu_{s}mgcos(\theta) so I have:
325t_{1} - mgsin(\theta) = \mu_{s}mgcos(\theta)
t_{1} = \frac{mg(sin(\theta)+\mu_{s}cos(\theta))}{325}
Now plugging in my values:
t_{1} = \frac{(50.8)(9.81)(sin(33)+(0.325)cos(33))}{325}
t_{1} = 1.25 s
So, after 1.25 seconds, the block moves up along the incline and the net force is:
F - mgsin(\theta) - \mu_{k}mgcos(\theta)
The impulse of the net force is:
\int_{t}^{t_{1}} (F-mgsin(\theta)-\mu_{k}cos(\theta)) = m(v-0)
\int_{t}^{t_{1}}(325t - mgsin(\theta)-\mu_{k}mgcos(\theta)) = mv
162.5(t^{2}-t_{1}^{2}) - mg(sin(\theta)-\mu_{k}cos(\theta))(t-t_{1}) = mv
162.5(t^{2}-(1.25)^{2})-177.4(t-1.25) = 123.95
162.5t^{2} - 177.4t - 126.76 = 0
When I solve this quadratic, I get t = 1.58 s. However, this answer is not correct and I am not quite sure where I went wrong. Any help is appreciated. Thanks.
Homework Equations
The Attempt at a Solution
I know when f < f_{max} = \mu_{s}mgcos(\theta), the system isn't moving, and the net force is:
F - mgsin(\theta) - f = 0.
f = F-mgsin(\theta) < \mu_{s}mgcos(\theta)
When t = t_{1}, f = \mu_{s}mgcos(\theta) so I have:
325t_{1} - mgsin(\theta) = \mu_{s}mgcos(\theta)
t_{1} = \frac{mg(sin(\theta)+\mu_{s}cos(\theta))}{325}
Now plugging in my values:
t_{1} = \frac{(50.8)(9.81)(sin(33)+(0.325)cos(33))}{325}
t_{1} = 1.25 s
So, after 1.25 seconds, the block moves up along the incline and the net force is:
F - mgsin(\theta) - \mu_{k}mgcos(\theta)
The impulse of the net force is:
\int_{t}^{t_{1}} (F-mgsin(\theta)-\mu_{k}cos(\theta)) = m(v-0)
\int_{t}^{t_{1}}(325t - mgsin(\theta)-\mu_{k}mgcos(\theta)) = mv
162.5(t^{2}-t_{1}^{2}) - mg(sin(\theta)-\mu_{k}cos(\theta))(t-t_{1}) = mv
162.5(t^{2}-(1.25)^{2})-177.4(t-1.25) = 123.95
162.5t^{2} - 177.4t - 126.76 = 0
When I solve this quadratic, I get t = 1.58 s. However, this answer is not correct and I am not quite sure where I went wrong. Any help is appreciated. Thanks.