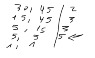- #1
kent davidge
- 933
- 56
Homework Statement
Police will be sent to conduct their work on a site which is a rectangular region of sides 3.9 km and 9.1 km. To make their work easier, the region will be divided into square regions, each one having the largest possible area, and such that their sum equals the original region. One police team will be sent to each such region. How many teams have to be sent?
Homework Equations
The Attempt at a Solution
(If you find this text bad looking that's because it was in my native language and I (poorly) translated it to English.)
So I think the problem is asking how many small regions we can divide the total region into such that the small regions have the largest possible area.
My attempt at a solution:
Let the total area be ##A = 3.9 \times 9.1 (km)^2##.
Let the small regions be ##a##. As their sum should equal the total area, we have ##ka = A, k \in \mathbb{N}##, or ##a = A / k##, and we must find the largest ##a## which is equal to the RHS of the last equality. This happens when ##k## assumes the smalest possible value, 1. But, no. That's not the answer. The official answer is 21. What can we do?