EmilyO89
- 4
- 0
1.
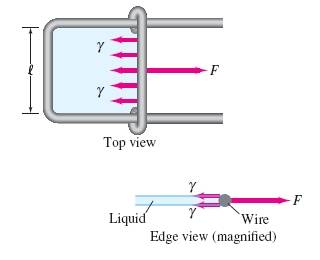
Calculate the force needed to move the wire in the figure (Figure 1) if it holds a soapy solution (surface tension is 0.025 N/m) and the wire is 16.0 cm long.
Express your answer to two significant figures and include the appropriate units.
 2.
2.
γ(surface tension) = F (force) / l (length)
3. My attempt at a solution
γ=F/l so γl=F
γ: 0.025 N/m
l: 16cm or 0.16m
0.025 N/m * 0.16m = 0.004 N or 4.0 * 10-3N
I know this must be ridiculously easy but I really can't figure out what I'm missing here. Do I need another equation to solve this problem? Am I messing up the units somehow?
Calculate the force needed to move the wire in the figure (Figure 1) if it holds a soapy solution (surface tension is 0.025 N/m) and the wire is 16.0 cm long.
Express your answer to two significant figures and include the appropriate units.
γ(surface tension) = F (force) / l (length)
3. My attempt at a solution
γ=F/l so γl=F
γ: 0.025 N/m
l: 16cm or 0.16m
0.025 N/m * 0.16m = 0.004 N or 4.0 * 10-3N
I know this must be ridiculously easy but I really can't figure out what I'm missing here. Do I need another equation to solve this problem? Am I messing up the units somehow?