How to calc sides of rectangle inside a rotated rectangle

[mhurkman]

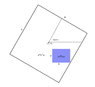
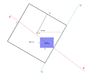
I'm hoping for some help as it has been 20 years since I last used trigonometry and Google has come up empty. I'm programming simple image editing software and for a crop function I need a formula to calculate the sides of the largest possible rectangle inside a rotated rectangle, given the coordinates of the center of the inner rectangle and aspect ratio of the sides. Largest is defined as the largest rectangle that touches but not exceeds any edge of the outer rectangle.

I know the length of the sides of the enclosing rectangle, L and W as well as angle of rotation, theta.
I also know the center coordinate of the inner rectangle (Px,Py) relative to the center of the enclosing rectangle as well as aspect ratio of the sides, p and q. Ie. p = r * q

I need this because the user is to freely rotate and drag the image (larger rectangle) and the crop window(smaller rectangle) must auto-adjust because the crop window of course cannot fall outside the image. Any help would be greatly appreciated.

Thanks,
Mark

 

[yuiop]

The solution is a little complicated and you might save yourself a lot of trouble by de-selecting any selected crop area when the user rotates the photograph and letting the user re-select the crop area once he has the desired rotation. One thing to consider is that if the crop area is in a corner before the rotation, its centre might be completely outside the photo boundary after a rotation. A lot of room for unexpected bugs in the programming here.

If you are determined to proceed, then here is a starter. First consider an imaginary line that passes diagonally through the crop area. (This is the red line R-R' in the attached diagram.) The equation for this line is:

y=Py-q/p*(x-Px)

The objective is to find where this line intersects the side of the photo. The side considered here is the lower edge which illustrated by the green line G-G' in the attached diagram. The equation for this line is:

y=(x-W/2*\sin(a))*tan(a)-W/2*cos(a)

At the intersection the above two equations are equal and can be solved for x to give:

x=\frac{Py+q/p*Px+W/2*(sin(a)*tan(a)+cos(a))}{tan(a)+q/p}

and the corresponding y value at the intersection is found by inserting this value for x into the equation for y above it. Now it is just a case of using Pythagorous to determine the distance from the intersect to the centre of the cropped area. You will have to repeat this process for all the other sides and find the intersection that is nearest to the centre of the cropped area and use this smallest value to determine the size of the cropped area. You will also have to check for the case when the intersections of the lines do not occur because they are parallel, before the calculation stage to avoid divide by zero errors.

Hope that helps.

 

[mhurkman]

Hello Yuiop,

Thank you so much for your reply. I understand your method, a clever approach. I see your point with Px,Py falling outside of the image area but since I will be recalculating the crop window continually as the user drags and rotates the image it should not happen.

Thanks a lot!
Mark

 

[yuiop]

Hello Yuiop,

Thank you so much for your reply. I understand your method, a clever approach. I see your point with Px,Py falling outside of the image area but since I will be recalculating the crop window continually as the user drags and rotates the image it should not happen.

Thanks a lot!
Mark

You are very welcome

I have edited my post because I accidentally swapped over the equations for the two lines but that is fixed now. You probably figured that out from the variables used. Other than that, the equations should be good. I tested them out in some plotting software and the line for the edge of the photograph rotates correctly when theta is adjusted and the intersection point of the two lines is correctly predicted.

 

[mhurkman]

Thanks, I will be implementing this over the weekend. Will let you know how it turns out.
Cheers,
Mark

 

[Veeranjaneyulu]

This looks like finding out the rectangular region after rotating the rectangle? If that is the case, could you please elaborate more on the values with some examples? It would be really good help if you can paste the implementation here.

Thanks,
Veeru.