How to Calculate Error on Beat Frequency?

[belgin fish]

I'm being asked to calculate the error on a beat frequency. The beat frequency was found to be 1/20.0s



The equation given is

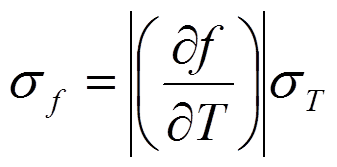
The thing is I am not really sure where to go from there or how to get the derivative of that, any help or pointing me in the right direction would be much appreciated.

 

[Delphi51]

Welcome to PF, Belgin.

You can only use that formula if you have the formula for f as a function of T and the error in T. It actually doesn't look like the right formula to me.

The beat frequency is the difference between two frequencies. Say you have two tones at 1000 Hz and 1100 Hz mixing together in your ear. You will hear 1000, 1100, the "beat" or difference between them and perhaps the sum. You would do 1100 - 1000 = 100 to calculate the beat frequency. If the accuracy on the 1100 and the 1000 is ± 10 Hz, then the beat could be anywhere from
(1100 - 10) - (1000 + 10) = 80 Hz to (1100+10) - (1000 - 10) = 120 Hz
so you would say it is 100 ± 20 Hz. I don't think it makes sense to use the differential equation in such a simple case - save it for a situation where you have multiplying at least.