sami23
- 69
- 1
Homework Statement
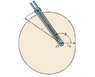
A cam has a shape that is described by the function r = r_0(2 - cos \theta), where r_0 = 2.25 ft. A slotted bar is attached to the origin and rotates in the horizontal plane with a constant angular velocity (\dot{\theta} dot) of 0.85 radians/s. The bar moves a roller weighing 25.6 lb along the cam's perimeter. A spring holds the roller in place; the spring's spring constant is 1.75 lb/ft. The friction in the system is negligible. When \theta = 102 degrees, what are F_r and F_\theta, the magnitudes of the cylindrical components of the total force acting on the roller?
Homework Equations
r = r_0(2 - cos \theta) = 2.25(2-cos102) = 4.9678 m
\dot{\theta} = 0.85 rad/s
\ddot{\theta} = 0 rad/s2
\dot{r} = (r_0sin\theta)(\dot{\theta}) = 2.25(.85)sin(102) = 1.87 m/s
\ddot{r} = (r_0cos\theta)(\dot{\theta})^2 + (r_0sin\theta)(\ddot{\theta}) = 2.25(.852)cos(102) = -0.338 m/s2
a_r = \ddot{r} - r(\dot{\theta})^2
a_\theta = r\theta + 2\dot{r}\dot{\theta}
F_r = W/g * a_r
F_\theta = W/g * a_\theta
F_s = ks (spring)
The Attempt at a Solution
a_r = \ddot{r} - r(\dot{\theta})^2 = -0.338 - 4.9678(.85^2) = -3.927 m/s2
a_\theta = r\theta + 2\dot{r}\dot{\theta} = 4.9678*0 + 2*1.87*.85 = 3.179 rad/s2
F_r = W/g * a_r = (25.6/32.2)*(-3.927) = 3.12 lb
F_\theta = W/g * a_\theta = (25.6/32.2)*(3.179) = 2.53 lb
But it's wrong and I didn't consider the spring force. How do I incorporate Fs? Please help. I'm stuck
Attachments
Last edited: