I How to calculate the mass of gas in a tank?

[Leopold89]

Dear community,

I have a question comparable to https://www.physicsforums.com/threads/calculating-the-mass-of-air-in-a-pressurised-air-tank.1053707/, but with some additional peculiarities.

My setup is:
1) I got a time series of gas pressure and temperature, with a time step of 2 minutes
2) I cannot measure the gas temperature, only the surrounding/room temperature
3) My gas can be either monoatomic or not and it has negligible contamination
4) The pressure is so large, that the gas turns into liquid
5) At arbitrary times during day time someone releases some gas from the tank, but not at night

Question: What is the remaining gas mass or particle number respectively?

My ansatz: First I can see that change in temperature will affect the pressure after some time delay, so I assume that should the tank contain a gas not at room temperature, the gas gets to room temperature after some time as well. This lag I can get from analysing the two time series.

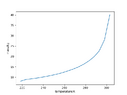
I would have assumed that I am moving along the p-T-curve when releasing gas, since some of the liquid evaporates until a new equilibrium between gas/vapour and liquid is reached, but the data shows I am well above this curve.
From this point onward I believe I am confusing myself. Now I know cannot use the ideal gas equation, because by releasing gas I am also converting liquid to gas/vapour, which should cool down the gas temperature below room temperature, followed by a heating phase, where the gas gets back to room temperature. As far as I understand I now need to somehow get the vapour volume, liquid volume, Gibbs energy and entropy to arrive at the remaining gas mass (or number of particles), right? I don't know how to get these.

 

[Chestermiller]

Are you taking into account the thermal inertia of the tank? Are you including the heat transfer rate between the tank contents and the air outside? What is the measured pressure and temperature vs time?

 

[Leopold89]

Are you taking into account the thermal inertia of the tank? Are you including the heat transfer rate between the tank contents and the air outside?

Other then by the time delay, no. The tank's heat transfer rate should be around 45 W/mK.

I have also included the time series. The pressure (blue, left axis) is in Pa and the temperature (red, right axis) in Kelvin. On x is the time series index, so multiplied by two minutes is the time.

 

[Chestermiller]

I think you need to get your feet wet with a simpler versions of the model first, before going to the full model. Would you be able to formulate a model where the tank is adiabatic, and where the thermal inertia of the tank itself is negligible?

 

[Leopold89]

Under these conditions I would use $p^{1-\gamma}T^{\gamma}=\mathrm{const}$, such that I would get $\tau_2:=\left( \frac{p_1}{p_2}\right)^{\frac{1}{\gamma} - 1} T_1$. Now that I got the temperature, I can get the particle number with $N=\frac{p_2V}{k_B\tau_2}$. Now that I got the temperature difference $T_2-\tau_2$ between the measured temperature $T_2$ and the gas temperature $\tau_2$, I can get the new pressure, after thermodynamic equilibrium is established with $p_\mathrm{eq}=\frac{Nk_BT_2}{V}$.
I used the fixed volume $V$ of the gas tank and I know the $\gamma$ from the type of gas in the container.

 

[Chestermiller]

Under these conditions I would use $p^{1-\gamma}T^{\gamma}=\mathrm{const}$, such that I would get $\tau_2:=\left( \frac{p_1}{p_2}\right)^{\frac{1}{\gamma} - 1} T_1$. Now that I got the temperature, I can get the particle number with $N=\frac{p_2V}{k_B\tau_2}$. Now that I got the temperature difference $T_2-\tau_2$ between the measured temperature $T_2$ and the gas temperature $\tau_2$, I can get the new pressure, after thermodynamic equilibrium is established with $p_\mathrm{eq}=\frac{Nk_BT_2}{V}$.
I used the fixed volume $V$ of the gas tank and I know the $\gamma$ from the type of gas in the container.

I thought you said you have two phases. What do you do in that case?

 

[Leopold89]

I thought you said you have two phases. What do you do in that case?

Ask the forum, because all I get is the Gibbs energy $G=U + pV - TS$, which I can rewrite as $\Delta U + p\Delta V - T\Delta S =0$, where $U$ is the inner energy and $S$ the entropy. Theoretically I can rewrite the liquid volume as $V-V_\mathrm{vapour}$ with $V_\mathrm{vapour}$ as the real root of $pV_\mathrm{vapour}^3-V_\mathrm{vapour}^2n_\mathrm{vapour}(bp+RT)+an^2V_\mathrm{vapour}-n_\mathrm{vapour}b=0$, where I used that pressure and temperature of vapour and liquid are equal. Then $\Delta V=2V_\mathrm{vapour}-V$ and I just replace one variable I don't know, $V_\mathrm{liquid}$, with another that I don't know, $n_\mathrm{vapour}$. I am not sure how to use the heat energy for condensation $Q=\frac{\mathrm{d}p}{\mathrm{d}T}(V_\mathrm{vapour}-V_\mathrm{liquid})T$, because I am not moving along the p-T-curve, right?

 

[Chestermiller]

For the adiabatic, reversible, 2 phase case, the open system version of the 1st law of thermodynamics tells us that $$dU=h_Vdm\tag{1}$$ where U is the internal energy of the tank contents, m is the mass of the tank contents ( dm is negative), and $h_V$ is the enthalpy per unit mass of the vapor. Eqn. 1 assumes that mass leaves the tank as a vapor through a valve at the top of the tank.

U is given by: $$U=m[(1-x)u_L+xu_V]\tag{2}$$where x is the mass fraction vapor in the tank, $u_L$ is the internal energy per unit mass of the liquid in the tank and $u_V$ is the internal energy per unit mass of the vapor in the tank.

The constant volume of the tank V is related to the specific volumes of liquid and vapor in the tank by: $$m[(1-x)v_L+xv_V]=V\tag{3}$$Solving Eqn. 3 for x gives:$$x=\frac{\frac{V}{m}-v_L}{v_V-v_L}\tag{4}$$OK so far?

 

[Leopold89]

I think so. If I understand correctly, I can then go and calculate $\frac{\partial U}{\partial m}=(1-x)u_L+xu_V -m\frac{\partial x}{\partial m}u_L +\frac{\partial x}{\partial m}u_Vm$ and get from this $u_V-u_L=\Delta u = \frac{(v_V-v_L)(u_L-h_V)}{v_L}$, where I used $\frac{\mathrm{d}U}{\mathrm{d}m}=h_V$ and $\Delta u$ related to $\Delta U$ in the above equation. But then I see no way forward, because the only equation linking enthalpy and entropy is the Gibbs energy, that I already used.

 

[Chestermiller]

I think so. If I understand correctly, I can then go and calculate $\frac{\partial U}{\partial m}=(1-x)u_L+xu_V -m\frac{\partial x}{\partial m}u_L +\frac{\partial x}{\partial m}u_Vm$ and get from this $u_V-u_L=\Delta u = \frac{(v_V-v_L)(u_L-h_V)}{v_L}$, where I used $\frac{\mathrm{d}U}{\mathrm{d}m}=h_V$ and $\Delta u$ related to $\Delta U$ in the above equation. But then I see no way forward, because the only equation linking enthalpy and entropy is the Gibbs energy, that I already used.

The next step is to substitute Eqn. 4 into Eqn.2. What do you get?

The saturated liquid and saturated vapor properties $u_L$, $u_V$, $h_V$, $v_V$, and v_L are known functions of temperature T. So we will first be deriving an equation for dT/dm, and then integrating this equation to obtain T as a function of the decreasing m.

 

[Leopold89]

I don't know if I am doing this right: starting with $h_V=u_V+pv_V$, $u_V=\frac{c_VR}{Mk_B}T$ and $v_V=\frac{RT}{Mp_V}$ I rewrite this as $\frac{\mathrm{d}T}{T}=\frac{M}{R}\mathrm{d}h_V-(\frac{c_V}{k_B}+\frac{1}{m})\mathrm{d}m+\frac{\mathrm{d}V}{V}+\frac{\mathrm{d}p}{p}$. Now I have to guess and say that I can use the specific heat capacity under constant pressure $\frac{\mathrm{d}H}{\mathrm{d}T}=c_p$, but because of $\frac{\mathrm{d}H}{\mathrm{d}T}=\frac{\mathrm{d}(mh_V)}{\mathrm{d}T}=\frac{h_V\mathrm{d}m+m\mathrm{d}h_V}{\mathrm{d}T}$ I cannot seperate the temperature from the $\mathrm{d}m$-term for the integration.

P.S.: Maybe the solution is $\mathrm{d}T=-\frac{h_v}{\frac{R}{M}-\frac{c_p}{m}}\mathrm{d}m \Rightarrow T=-h_v\frac{c_p \mathrm{ln}(c_p-\frac{R}{M}m) +\frac{R}{M}m}{\frac{R^2}{M^2}}$, where $M$ is the molar mass and $R$ the molar gas constant.

 

[Chestermiller]

I get $$U=\frac{u_V-u_L}{v_V-v_L}V+\frac{v_Vu_L-v_Lu_V}{v_V-v_L}m$$

 

[Leopold89]

Yes, that was

substitute Eqn. 4 into Eqn.2

But from that point onward I don't understand. You said that $u_L$ and $v_L$ are known, but I don't know the formulas for liquids.

 

[Chestermiller]

Yes, that was


But from that point onward I don't understand. You said that $u_L$ and $v_L$ are known, but I don't know the formulas for liquids.

If it is water, then. you have the Steam Tables, which give all there functions. For other pure substances like refrigerants and many others, there are tables for these too. Are you familiar with the Steam Tables. They are in most Thermo books.

The vapor does not have to be ideal gas.

 

[Chestermiller]

From post #12, the internal energy has the form $$U=F_1(T)V+F_2(T)m$$ where F1 and F2 are known functions of T. So, from the first law, $$F'_1V+F'_2m+F_2dm=h_vdm$$or $$\frac{dm}{dT}=F_3V+F_4m\tag{5}$$where $$F_3(T)=\frac{F'_1}{h_v-F_2}$$ and $$F_4(T)=\frac{F'_2}{h_v-F_2}$$All that needs to be done is to integrate Eqn. 5 numerically with respect to T.

 

[Leopold89]

I did not know of steam tables before.

I still have problems with two points:
1) I looked for water steam for example (https://roymech.org/Related/Thermos/Thermos_Steam_Tables_2.html).
So by integrating you mean solving a inhomogenous first order differential equation numerically? For that I would need an initial value, so a fresh gas tank, right?
2) A problem I have is that I could derive $\frac{\mathrm{d}U}{\mathrm{d}m}=h_V=u_V+pv_V=F_2(T)$ and from that deduce $v_V=0$ by comparing coefficients, which is false, but what am I doing wrong?

 

[Chestermiller]

I did not know of steam tables before.

I still have problems with two points:
1) I looked for water steam for example (https://roymech.org/Related/Thermos/Thermos_Steam_Tables_2.html).
So by integrating you mean solving a inhomogenous first order differential equation numerically?

yes

For that I would need an initial value, so a fresh gas tank, right?

That wouldn't be a problem if you know the equation of state.

2) A problem I have is that I could derive $\frac{\mathrm{d}U}{\mathrm{d}m}=h_V=u_V+pv_V=F_2(T)$ and from that deduce $v_V=0$ by comparing coefficients, which is false, but what am I doing wrong?

This is not done correctly. The correct derivation is in post #15. U is a function of both m and T and its differential involves dm and dT.

 

[Chestermiller]

Show using the Clapeyron equation that $$F_1=T\frac{dP}{dT}-P$$ and that $$F_2=h_v-\left(T\frac{dP}{dT}\right)v_V$$where P is the equilibrium vapor pressure at temperature T.

 

[Leopold89]

First one:
$F_1=\frac{\Delta u}{\Delta v}\frac{m}{m}$
$F_1=\frac{\Delta U}{\Delta V}=\frac{T\Delta S - p\Delta V}{\Delta V}$
$F_1=T\frac{\mathrm{d}p}{\mathrm{d}T}-p$

Second:
$F_2=\frac{u_Lv_V-u_Vv_L}{\Delta v}$
$=\frac{u_Lv_V-u_Vv_L + u_Vv_V-u_Vv_V}{\Delta v}$
$=\frac{u_V\Delta V -v_V\Delta U}{\Delta V}$
$=h_V-\frac{p\Delta V + \Delta U}{\Delta V}v_V$
$=h_V-\frac{T\Delta S}{\Delta V}v_V$
$=h_V-T\frac{\Delta p}{\Delta T}v_V$

One other question appeared while I was looking for the steam tables: Some tables do not show the internal energy, but instead the entropy. Would I then use $F_1=T\frac{\Delta s}{\Delta v}-p$ and analogously for $F_2$?

 

[Chestermiller]

First one:
$F_1=\frac{\Delta u}{\Delta v}\frac{m}{m}$
$F_1=\frac{\Delta U}{\Delta V}=\frac{T\Delta S - p\Delta V}{\Delta V}$
$F_1=T\frac{\mathrm{d}p}{\mathrm{d}T}-p$

Second:
$F_2=\frac{u_Lv_V-u_Vv_L}{\Delta v}$
$=\frac{u_Lv_V-u_Vv_L + u_Vv_V-u_Vv_V}{\Delta v}$
$=\frac{u_V\Delta V -v_V\Delta U}{\Delta V}$
$=h_V-\frac{p\Delta V + \Delta U}{\Delta V}v_V$
$=h_V-\frac{T\Delta S}{\Delta V}v_V$
$=h_V-T\frac{\Delta p}{\Delta T}v_V$

One other question appeared while I was looking for the steam tables: Some tables do not show the internal energy, but instead the entropy. Would I then use $F_1=T\frac{\Delta s}{\Delta v}-p$ and analogously for $F_2$?

All the ones I am familiar with have T, P, v, u, h,and s for saturated liquid and vapor.

 

[Chestermiller]

The variables m and V in Eqn. 5 of post #15 can be combined into a single variable $\rho=m/V$ which represents the average density of the combination of vapor and liquid at any time:$$\frac{d\rho}{dT}=F_3+F_4\rho\tag{5}$$This eliminates the mass and volume as separate variables.

 

[Leopold89]

Maybe I was not using the term right, but I meant the tables for other gases than water. For example the table for Argon I found only had the densities and vapour enthalpy for given temperature and pressure. In case of water I have indeed every variable. If you have a source with better tables, can you please link it to me?

In the next step with the thermal inertia of the tank, I believe I would have to construct a system of differential equations, one for $T_\mathrm{tank}(t)$ based on the heat diff. equation with both the inside as well as the room temperature as external influence, then one for the inside $T_\mathrm{inside}(p, t)$ using the tables and lastly $m(p,T)$ similar to post #15, right?

 

[Chestermiller]

Maybe I was not using the term right, but I meant the tables for other gases than water. For example the table for Argon I found only had the densities and vapour enthalpy for given temperature and pressure. In case of water I have indeed every variable. If you have a source with better tables, can you please link it to me?

Are you really doing argon. If you cannot find the tables on a substance, you will have to create your own (or derive analytical expressions for the required saturated properties).

I suggest you do a sample calculation using water to see how this all plays out and what to expect.

In the next step with the thermal inertia of the tank, I believe I would have to construct a system of differential equations, one for $T_\mathrm{tank}(t)$ based on the heat diff. equation with both the inside as well as the room temperature as external influence, then one for the inside $T_\mathrm{inside}(p, t)$ using the tables and lastly $m(p,T)$ similar to post #15, right?

Before modeling the problem with the thermal inertia included, you should first check in a model calculation without inertia to see if it would significant. This could be done by assuming that the tank attains the same temperature history as the gas and comparing the changes in internal energy.

 

[Leopold89]

I have now a curve for $\mathrm{CO}_2$, because the implementation was easier than water. But I had to set the initial value at a somewhat arbitrary value of 8kg.

 

[Chestermiller]

I have now a curve for $\mathrm{CO}_2$, because the implementation was easier than water. But I had to set the initial value at a somewhat arbitrary value of 8kg.

The mass and temperature are decreasing as the tank expels gas, not increasing. The curve you presented would be for an initial mass of ~40 kg (if it is correct).

 

[Leopold89]

The mass and temperature are decreasing as the tank expels gas, not increasing. The curve you presented would be for an initial mass of ~40 kg (if it is correct).

I implemented it with the python odeint and since my table is sorted with respect to temperature, my initial value is with respect to the lowest temperature. I have also plotted the 3D graph with temperature and pressure, where I observe what you said. As I release gas, or decrease pressure, the temperature and mass falls.

 

[Chestermiller]

I implemented it with the python odeint and since my table is sorted with respect to temperature, my initial value is with respect to the lowest temperature. I have also plotted the 3D graph with temperature and pressure, where I observe what you said. As I release gas, or decrease pressure, the temperature and mass falls.

You should also show a plot of he mass fraction of vapor x as a function of temperature and or mass. Note that the mass fraction vapor in the tank is an initial condition for the calculation.

 

[Leopold89]

Here is the plot for x in dependance of mass and temperature for $\mathrm{CO}_2$. I had to play with my initial condition, because unfortunately I cannot measure it right now. So I adjusted it until x was between 0 and 1. The initial mass, as you can see, is now at 2kg instead of the previous 8kg, else I got negative x.
But all I learned from this is that it is "garbage in, garbage out".

But maybe you can give me realistic initial conditions for a water steam tank and then I do it with water.

 

[Chestermiller]

Here is the plot for x in dependance of mass and temperature for $\mathrm{CO}_2$. I had to play with my initial condition, because unfortunately I cannot measure it right now. So I adjusted it until x was between 0 and 1. The initial mass, as you can see, is now at 2kg instead of the previous 8kg, else I got negative x.
But all I learned from this is that it is "garbage in, garbage out".

But maybe you can give me realistic initial conditions for a water steam tank and then I do it with water.

You need to integrate in the negative m direction. In your integrator, make the final temperature less than the initial temperature.

For water, try an initial saturation pressure of 5 bars and an initial mass fraction vapor of 0.9.

 

[Leopold89]

Here I have the solution for water with an initial pressure of 5 bars and $x_0=0.9$, where I used the steam table here. I have also adjusted the integration to your direction.
I am rather sure that this is wrong, because I need an initial mass and a fixed volume.

 

[Chestermiller]

Here I have the solution for water with an initial pressure of 5 bars and $x_0=0.9$, where I used the steam table here. I have also adjusted the integration to your direction.
I am rather sure that this is wrong, because I need an initial mass and a fixed volume.

As I said in post #21, you don't need the mass and volume separately, only the mass divided by volume (the average density). You specified the initial state, so you know the initial mass fractions of liquid and vapor, the specific volumes of saturated liquid and gas, and thus the mass divided by tank volume. See Eqn. 3 of post #8.

 

[Leopold89]

Here is the new curve for water. It looks plausible, since the more gas I release from the tank, the more vapour I expect.

 

[Leopold89]

Now I am actually more confused. I thought the vapour-liquid temperature will get in balance with room temperature after some time, but now I see that my solution above may not even be defined for a measured pressure at room temperature. Does this mean I have to measure x at these $p,T$ and solve the same differential equation but in two dimensions with my expanded steam table?

Can you show me the thermal inertia of the tank, too, please?

 

[Chestermiller]

Now I am actually more confused. I thought the vapour-liquid temperature will get in balance with room temperature after some time, but now I see that my solution above may not even be defined for a measured pressure at room temperature.

What do you mean by this? Do you mean that it all turns to vapor or liquid at a certain point? What is happening that you say this?

Does this mean I have to measure x at these $p,T$ and solve the same differential equation but in two dimensions with my expanded steam table?

No. please answer my previous question..

Can you show me the thermal inertia of the tank, too, please?

The thermal inertia of the tank is its mass times its heat capacity.

 

[Leopold89]

What do you mean by this? Do you mean that it all turns to vapor or liquid at a certain point? What is happening that you say this?

No. What I mean is that I could for example measure a temperature of 25°C with a pressure of 10bar, then 26°C with a pressure of 8bar, 24°C with 4bar, 25°C with 2bar and so on. So what I mean is that my measurements may not be close to the line I calculated in post #32.

 

[Chestermiller]

No. What I mean is that I could for example measure a temperature of 25°C with a pressure of 10bar, then 26°C with a pressure of 8bar, 24°C with 4bar, 25°C with 2bar and so on. So what I mean is that my measurements may not be close to the line I calculated in post #32.

Is this what you are measuring inside the tank?

 

[Leopold89]

Somwhat yes. I have also included a plot of my data of one gas tank.

Edit: I think I understand now. The integrated curve is the same as the p-T-curve in the phase diagrams, so once I am above or below it, the model has to change between a pure liquid, a liquid-vapour mixture and a pure vapour/gas, right?

 

[Chestermiller]

Somwhat yes. I have also included a plot of my data of one gas tank.

Edit: I think I understand now. The integrated curve is the same as the p-T-curve in the phase diagrams, so once I am above or below it, the model has to change between a pure liquid, a liquid-vapour mixture and a pure vapour/gas, right?

Yes.

 

[Leopold89]

I am afraid I still don't understand. I attached here a mass plot of a tank with only vapour content. I used the ideal gas equation corrected for van der Waals forces, but not the thermal inertia. Now what we see is a contradiction with the experiment: You can only release gas, not introduce it other by replacing the whole tank, what did not happen during this measurement.

 

[Chestermiller]

The first law open system equation for introducing gas is different from the equation we used for removing gas. It should read $$dU=h_{out}dm$$ where $h_{out}$ is the enthalpy of the gas outside the valve.

 

[Leopold89]

The first law open system equation for introducing gas is different from the equation we used for removing gas. It should read $$dU=h_{out}dm$$ where $h_{out}$ is the enthalpy of the gas outside the valve.

But I am not introducing gas, only releasing.

 

[Chestermiller]

But I am not introducing gas, only releasing.

So the temperature rises because of heat flow from the surroundings?

 

[Leopold89]

The (room) temperature is the same as in post #3, so the temperature change is slower than the oscillation in the mass. The pressure data shows these weird peaks and only for this one gas ($\mathrm{CO}_2$), not the others, but I still get unplausible mass increases for the other gases, just not as dramatic as for $\mathrm{CO}_2$. If the surrounding would give off heat, then I would have expected to see these peaks in other gas tanks as well, but I don't.

 

[Juanda]

@Leopold89 I have been watching the thread for a while and I think it's very interesting. I'm not nearly as experienced as @Chestermiller but maybe the input can still be useful.

You mentioned you're mainly interested in knowing the mass remaining in the tank. Before diving into thermodynamic properties and equations, would it be possible just to weigh the loaded and unloaded tank? Or maybe knowing how much you put in and later weighing the discharged gas into a reservoir so you can know how much remains.

If it's not possible, let me first say that the information available is very limited. Knowing extensive properties (mass, internal energy [J], etc) from only intensive properties (pressure, density/specific volume, temperature, etc) is very hard. I'm not even sure is possible. You may be able to fully define the thermodynamic state of a substance but you don't know how much of it there is. At some point, some extensive information must be added.

In this scenario, only the pressure is known which we can assume is uniform within the tank. Even the temperature of the content isn't really measured since you said it's measured in the room $(\tau)$ and not in the tank $(T)$. As you mentioned in point (2) in the OP, why isn't it possible to measure the temperature inside? I guess it could be derived from other equations but it makes everything a little more complex than it already is and more assumptions are necessary to be able to run the numbers. If you end up being able to install temperature sensors, I'd install a bunch of them at different locations (somewhere in the middle, the bottom, near the valves, etc.). I'd assume the temperature is uniform though just like the pressure although it depends on how rapid the process is. If it's very quick, the area near the valve will be different and, if there is a mixture of liquid and gas, they might not be in equilibrium where they would have the same pressure and temperature.

Assuming none of what I said before is possible, could you characterize the valve? That way, the output mass could be derived from the properties of the gasses.

(NOTE: For all my calculations I'll assume the properties to be uniform so pressure and temperature are the same for everything inside the tank although internal energy, enthalpy and so on will depend on whether it's liquid or gas. Basically, I'm assuming the content is going from A→B through equilibrium states.)
If the full content of the tank were a gas, the approximation to find the mass isn't too difficult depending on how much accuracy you want. Ideal gas law will give you a quick result since you already know the pressure, the temperature, and the total volume (this would be your extensive property) of the tank. As long as you check from the property tables that you don't have a saturated mixture you could use the simple ideal gas law (or use tabulated values).
$$PV = mRT \rightarrow m = \frac{PV}{RT}$$
So the problem lies in the saturated mixture of which we don't know the proportion of gas to liquid or "vapor quality" $x$. I'll focus on modeling the problem for the time when that mixture is in the tank. As time goes on, more liquid will continue to evaporate until it's 100% gas and you switch to the model previously mentioned.
Using a control volume which is the tank, I'll apply the conservation of mass and conservation of energy.

CONSERVATION OF MASS
$$\frac{d}{dt}\int_{CV}\rho dV=\dot{m}_{in}-\dot{m}_{out}$$
In this problem, gas is only coming out of the tank so we can make $\dot{m}_{in}=0$. Because of the sign convention used, $\dot{m}_{out}$ will be positive.
The integral on the left side can be evaluated as:
$$\int_{CV}\rho dV = m_{g}+m_{f}$$
Where $m_g$ is the mass of saturated gas in the mixture and $m_f$ is the mass of the saturated fluid.
The end result of the conservation of mass applied on the control volume is:
$$\frac{dm_{g}}{dt}+\frac{dm_{f}}{dt}=-\dot{m}_{out}$$
(I have intentionally not used the · sign for derivatives on the left side because, although it's mass changing over time, that's not really "flow".
The functions $m_g(t)$ and $m_f(t)$ are what we need. To calculate them, we need to know more about the output mass flow $\dot{m}_{out}$. If you experimentally measure it, then that's it. Use that function. If you can't measure it but you can characterize the valve, then the mass flow should be possible to be expressed using the characteristics of the valve and the properties of the gas. If you can't characterize the valve, you'll have to solve the problem several times using different values for the characteristics of the valve and checking if the results are similar to the experimental values of $P$ and $T$ that you already have.
Anyway, we have two functions so we need two boundary conditions, which will be the initial masses of the system, and two equations. For the second equation, we use conservation of energy.

CONSERVATION OF ENERGY
$$\frac{dE_{CV}}{dt}=\dot{Q}-\dot{W}+\dot{m}_{in}h_{in}-\dot{m}_{out}h_{out}$$
From that equation, we know we're not introducing or extracting work in the system so $\dot{W}=0$.
The heat input $\dot{Q}$ will be a function of the temperature difference and the thermal resistance. The temperature difference I assume is known from the room temperature which I consider constant and whatever function you're using to find out the temperature inside the tank from the value $(\tau)$. You mentioned the thermal resistance in another post so it's known too.
The input flow we have already said it's $\dot{m}_{in}=0$.
The output flow $\dot{m}_{out}$ is a function whose properties have already been discussed in the previous equation.
The enthalpy of the output $h_{out}$ flow is known since you know the temperature and pressure of the saturated mix at any moment so you can find it in tables (notice that it'll change as time passes).
Lastly, the energy in the control volume $E_{CV}$ will be only the internal energy of the gas and liquid because it's not flowing. It can be expressed as:
$$\frac{dE_{CV}}{dt}=\frac{dU_{g}}{dt}+\frac{dU_{l}}{dt}$$
Since it's a saturated mixture, it's going through a phase change. Therefore, its pressure and temperature should be constant.
$$\frac{dU_{g}}{dt}=\frac{d(cmT)_{g}}{dt}=c_g T_g \frac{dm_{g}}{dt}$$
$$\frac{dU_{l}}{dt}=\frac{d(cmT)_{l}}{dt}=c_l T_l \frac{dm_{l}}{dt}$$
As a result, the expression for the conservation of energy during the discharge of the saturated mixture is:
$$c_g T_g \frac{dm_{g}}{dt}+c_l T_l \frac{dm_{l}}{dt}=\dot{Q}-\dot{m}_{out}h_{out}$$

That system of differential equations should be solvable from the information I described. For greater clarity, here are the two equations together.
$$\frac{dm_{g}}{dt}+\frac{dm_{f}}{dt}=-\dot{m}_{out}$$
$$c_g T_g \frac{dm_{g}}{dt}+c_l T_l \frac{dm_{l}}{dt}=\dot{Q}-\dot{m}_{out}h_{out}$$


PS:
I'm aware my approach seems different from what you've been doing in the thread. Maybe what I'm doing is oversimplified and won't capture the actual behavior you're observing experimentally. Still, since you're getting some strange artifacts from your current approach to the problem, it might still be worth trying this method and comparing the results. I assume the differential equations should produce a non-stopping decline in mass within the tank as long as there is a mass output. Pressure and temperature will remain constant until there is no more liquid and then you switch to ideal gas or something similar because your experimental data is enough to determine the mass without having to solve a differential equation.
By the way, are you sure you have a saturated mixture in the tank? I think you haven't shared what's the chemical inside in detail so I couldn't check with some tables (if there are any for that compound).
From your data, I'm not sure if it's OK to assume the properties remain constant during the phase change although it's impossible to judge without knowing how are the discharges (how much it opens, for how long, etc.). In the red arrows, I'd expect to see a more constant behavior because the amount of liquid there should be greatest. However, I only see a constant behavior in the blue arrows. Since the temperature keeps dropping slightly, I assume it's discharging but the pressure is not changing. In theory, temperature should not change either within the chamber but you're not measuring at that point but in the room. Also, as previously mentioned, if the process is too violent the tank's content won't have time to equalize. Still, maybe there is liquid and the process is not as violent at the blue arrows so that phase change can be more easily observed.

The condensed amount might be very small. Have you tried ignoring it and comparing the results to your experimental data? It might give you a good enough approximation.

 

[Juanda]

That system of differential equations should be solvable from the information I described. For greater clarity, here are the two equations together.
$$\frac{dm_{g}}{dt}+\frac{dm_{f}}{dt}=-\dot{m}_{out}$$
$$c_g T_g \frac{dm_{g}}{dt}+c_l T_l \frac{dm_{l}}{dt}=\dot{Q}-\dot{m}_{out}h_{out}$$

I'm now realizing that, as the discharge happens, the liquid will evaporate while temperature and pressure remain constant due to the phase change. Then, once it's all gas, its expansion will start cooling down the remaining gas.
Could that cooling condense it back?
Picture source: Thermodynamics_ An Engineering Approach by Yunus A. Çengel, Michael A. Boles and Mehmet Kanoglu from McGraw Hill (2023)

What I described in the previous post is using differential equations to model the straight segment. Once you're out of the bell (it's all gas), I thought it'd be fine to use the ideal gas law or something similar to find the remaining gas within the tank from the experimental data but I don't know if the path it follows is the red line bordering the bell or something else like the blue line. I don't think it'd be able to get inside the bell again due to its own cooling though.
Maybe it'd be interesting to model the behavior outside the bell with differential equations too to see how close to the experimental data you can get it instead of directly using the experimental data (PTV) to try to get the mass inside the tank by using ideal gas law.

 

[Chestermiller]

@Leopold89 I have been watching the thread for a while and I think it's very interesting. I'm not nearly as experienced as @Chestermiller but maybe the input can still be useful.

You mentioned you're mainly interested in knowing the mass remaining in the tank. Before diving into thermodynamic properties and equations, would it be possible just to weigh the loaded and unloaded tank? Or maybe knowing how much you put in and later weighing the discharged gas into a reservoir so you can know how much remains.

If it's not possible, let me first say that the information available is very limited. Knowing extensive properties (mass, internal energy [J], etc) from only intensive properties (pressure, density/specific volume, temperature, etc) is very hard. I'm not even sure is possible. You may be able to fully define the thermodynamic state of a substance but you don't know how much of it there is. At some point, some extensive information must be added.

As I said in a previous post, extensive information is not necessary if you calculate the mass per unit volume. All other information is present in the thermodynamic tables for the substance (e.g., the steam tables for water).

In this scenario, only the pressure is known which we can assume is uniform within the tank. Even the temperature of the content isn't really measured since you said it's measured in the room $(\tau)$ and not in the tank $(T)$. As you mentioned in point (2) in the OP, why isn't it possible to measure the temperature inside? I guess it could be derived from other equations but it makes everything a little more complex than it already is and more assumptions are necessary to be able to run the numbers. If you end up being able to install temperature sensors, I'd install a bunch of them at different locations (somewhere in the middle, the bottom, near the valves, etc.). I'd assume the temperature is uniform though just like the pressure although it depends on how rapid the process is. If it's very quick, the area near the valve will be different and, if there is a mixture of liquid and gas, they might not be in equilibrium where they would have the same pressure and temperature.

Assuming none of what I said before is possible, could you characterize the valve? That way, the output mass could be derived from the properties of the gasses.

If the full content of the tank were a gas, the approximation to find the mass isn't too difficult depending on how much accuracy you want. Ideal gas law will give you a quick result since you already know the pressure, the temperature, and the total volume (this would be your extensive property) of the tank. As long as you check from the property tables that you don't have a saturated mixture you could use the simple ideal gas law (or use tabulated values).
$$PV = mRT \rightarrow m = \frac{PV}{RT}$$
So the problem lies in the saturated mixture of which we don't know the proportion of gas to liquid or "vapor quality" $x$. I'll focus on modeling the problem for the time when that mixture is in the tank. As time goes on, more liquid will continue to evaporate until it's 100% gas and you switch to the model previously mentioned.
Using a control volume which is the tank, I'll apply the conservation of mass and conservation of energy.

CONSERVATION OF MASS
$$\frac{d}{dt}\int_{CV}\rho dV=\dot{m}_{in}-\dot{m}_{out}$$
In this problem, gas is only coming out of the tank so we can make $\dot{m}_{in}=0$. Because of the sign convention used, $\dot{m}_{out}$ will be positive.
The integral on the left side can be evaluated as:
$$\int_{CV}\rho dV = m_{g}+m_{f}$$
Where $m_g$ is the mass of saturated gas in the mixture and $m_f$ is the mass of the saturated fluid.
The end result of the conservation of mass applied on the control volume is:
$$\frac{dm_{g}}{dt}+\frac{dm_{f}}{dt}=-\dot{m}_{out}$$

(I have intentionally not used the · sign for derivatives on the left side because, although it's mass changing over time, that's not really "flow".
The functions $m_g(t)$ and $m_f(t)$ are what we need. To calculate them, we need to know more about the output mass flow $\dot{m}_{out}$. If you experimentally measure it, then that's it. Use that function. If you can't measure it but you can characterize the valve, then the mass flow should be possible to be expressed using the characteristics of the valve and the properties of the gas. If you can't characterize the valve, you'll have to solve the problem several times using different values for the characteristics of the valve and checking if the results are similar to the experimental values of $P$ and $T$ that you already have.
Anyway, we have two functions so we need two boundary conditions, which will be the initial masses of the system, and two equations. For the second equation, we use conservation of energy.

CONSERVATION OF ENERGY
$$\frac{dE_{CV}}{dt}=\dot{Q}-\dot{W}+\dot{m}_{in}h_{in}-\dot{m}_{out}h_{out}$$
From that equation, we know we're not introducing or extracting work in the system so $\dot{W}=0$.
The heat input $\dot{Q}$ will be a function of the temperature difference and the thermal resistance. The temperature difference I assume is known from the room temperature which I consider constant and whatever function you're using to find out the temperature inside the tank from the value $(\tau)$. You mentioned the thermal resistance in another post so it's known too.
The input flow we have already said it's $\dot{m}_{in}=0$.
The output flow $\dot{m}_{out}$ is a function whose properties have already been discussed in the previous equation.
The enthalpy of the output $h_{out}$ flow is known since you know the temperature and pressure of the saturated mix at any moment so you can find it in tables (notice that it'll change as time passes).

You have not specified whether the output flow from the tank is pure vapor or a combination of vapor and liquid (say at the mass fractions as in the tank). I assumed that the process is taking place slowly in a gravitational field, and that the output is saturated vapor only.

Lastly, the energy in the control volume $E_{CV}$ will be only the internal energy of the gas and liquid because it's not flowing. It can be expressed as:
$$\frac{dE_{CV}}{dt}=\frac{dU_{g}}{dt}+\frac{dU_{l}}{dt}$$
Since it's a saturated mixture, it's going through a phase change. Therefore, its pressure and temperature should be constant.

This is only true if the system is forced to be at constant pressure. In a case like this, of constant total volume, both the temperature and the pressure are changing along the equilibrium saturation line and the proportions of vapor and liquid are changing.

$$\frac{dU_{g}}{dt}=\frac{d(cmT)_{g}}{dt}=c_g T_g \frac{dm_{g}}{dt}$$
$$\frac{dU_{l}}{dt}=\frac{d(cmT)_{l}}{dt}=c_l T_l \frac{dm_{l}}{dt}$$

These equations are not correct because the temperature and pressure is changing along with the proportion of liquid and vapor. Also, the heat of vaporization is not included. I derived the correct energy balance in an early post, although I had tentatively assumed that the heat transfer was negligible.

As a result, the expression for the conservation of energy during the discharge of the saturated mixture is:
$$c_g T_g \frac{dm_{g}}{dt}+c_l T_l \frac{dm_{l}}{dt}=\dot{Q}-\dot{m}_{out}h_{out}$$

See my comments above.

That system of differential equations should be solvable from the information I described. For greater clarity, here are the two equations together.
$$\frac{dm_{g}}{dt}+\frac{dm_{f}}{dt}=-\dot{m}_{out}$$
$$c_g T_g \frac{dm_{g}}{dt}+c_l T_l \frac{dm_{l}}{dt}=\dot{Q}-\dot{m}_{out}h_{out}$$


PS:
I'm aware my approach seems different from what you've been doing in the thread. Maybe what I'm doing is oversimplified and won't capture the actual behavior you're observing experimentally. Still, since you're getting some strange artifacts from your current approach to the problem, it might still be worth trying this method and comparing the results. I assume the differential equations should produce a non-stopping decline in mass within the tank as long as there is a mass output. Pressure and temperature will remain constant until there is no more liquid and then you switch to ideal gas or something similar because your experimental data is enough to determine the mass without having to solve a differential equation.
By the way, are you sure you have a saturated mixture in the tank? I think you haven't shared what's the chemical inside in detail so I couldn't check with some tables (if there are any for that compound).

If you correct the few points that I indicated above, you might get an approximation this way. But first see the derivation that I gave in my posts, which only omits the heat exchange with the surroundings.

From your data, I'm not sure if it's OK to assume the properties remain constant during the phase change although it's impossible to judge without knowing how are the discharges (how much it opens, for how long, etc.).

The temperature and pressure do not remain constant during the phase change in a constant volume tank.

 

[Chestermiller]

I'm now realizing that, as the discharge happens, the liquid will evaporate while temperature and pressure remain constant due to the phase change. Then, once it's all gas, its expansion will start cooling down the remaining gas.

This is not correct because the temperature and pressure both change in this constant tank volume situation.

 

[Juanda]

Thanks for the corrections @Chestermiller. I'll read the thread again and try the problem from another angle.
The reason I tried this in the first place is that I couldn't understand some points in the thread though.

I have a few comments about your last posts.

As I said in a previous post, extensive information is not necessary if you calculate the mass per unit volume. All other information is present in the thermodynamic tables for the substance (e.g., the steam tables for water).

Yeah but OP said he's interested in knowing the mass inside the tank, right? At some point, some extensive property must be added. For example, assuming an initial mass and data from the output mass.

You have not specified whether the output flow from the tank is pure vapor or a combination of vapor and liquid (say at the mass fractions as in the tank). I assumed that the process is taking place slowly in a gravitational field, and that the output is saturated vapor only.

True. I didn't write it explicitly but I assumed the mass output was saturated vapor while in the chamber remains saturated vapor and saturated liquid whose properties can all be found in tables.

(This is about my claim about temperature and pressure remaining constant due to the phase change)

This is only true if the system is forced to be at constant pressure. In a case like this, of constant total volume, both the temperature and the pressure are changing along the equilibrium saturation line and the proportions of vapor and liquid are changing.

These equations are not correct because the temperature and pressure is changing along with the proportion of liquid and vapor. Also, the heat of vaporization is not included. I derived the correct energy balance in an early post, although I had tentatively assumed that the heat transfer was negligible.

The temperature and pressure do not remain constant during the phase change in a constant volume tank.

Can you explain why the pressure and temperature are not constant during the phase change? It's one of those things I remember as a golden rule during phase change. I admit I was surprised about the temperature and pressure graphs supplied by @Leopold89 but I thought I didn't see it happening there because either the phenomenon was too violent so the mix is not in equilibrium, the sensors were not reading correctly, or any other complicated reason that often arises when dealing with real-world problems.


Lastly, @Leopold89 you are interested in knowing the remaining mass in the tank. We have already stated that the problem occurs when there is a mixture of gas and liquid inside because your sensors don't provide enough information by themselves. I tried to propose some engineering solutions that don't involve complicated calculations such as weighing the tank but that might be difficult. How about installing a floater so you can know how much liquid there is inside? For example:

Once the volume of liquid is known, you'd easily find the mass in the tank once the properties of both liquid and gas are known.

 

[Chestermiller]

Thanks for the corrections @Chestermiller. I'll read the thread again and try the problem from another angle.
The reason I tried this in the first place is that I couldn't understand some points in the thread though.

I have a few comments about your last posts.


Yeah but OP said he's interested in knowing the mass inside the tank, right? At some point, some extensive property must be added. For example, assuming an initial mass and data from the output mass.

The required extensive property is the constant tank volume V.

True. I didn't write it explicitly but I assumed the mass output was saturated vapor while in the chamber remains saturated vapor and saturated liquid whose properties can all be found in tables.


Can you explain why the pressure and temperature are not constant during the phase change? It's one of those things I remember as a golden rule during phase change. I admit I was surprised about the temperature and pressure graphs supplied by @Leopold89 but I thought I didn't see it happening there because either the phenomenon was too violent so the mix is not in equilibrium, the sensors were not reading correctly, or any other complicated reason that often arises when dealing with real-world problems.

What you remember is that, for a phase change at constant pressure, the temperature is constant.

 

[Juanda]

The required extensive property is the constant tank volume V.

But that's only enough if we knew the content is 100% gas because it'd occupy the full volume or 100% liquid as long as it is at 100% capacity.

What you remember is that, for a phase change at constant pressure, the temperature is constant.

That's probably it. I'm a little rusty on this but, from what I remember, power cycles involving vapor always have that constant behavior inside the bell.
I checked THE book (Çengel) again and the constant pressure is mentioned. I assumed the constant pressure (and temperature) was a result of the phase change but the phase change is actually not even mentioned. So it is imposing a constant pressure inside the bell that is causing the constant temperature during that part of the process.

I don't know how to describe a phase change where the pressure is not held constant then. I feel I need more information.