Offline1
- 3
- 0
Homework Statement
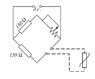
A resistance thermometer bridge circuit shown below has a
designed maximum temperature of 150°C, ignoring the effects of
connecting wire resistance. If the connecting loop is 200 m
determine the smallest gauge (swg) of copper wire which must be
used if the indicated maximum temperature is to be less than 151°C.
The temperature coefficient of resistance of the thermometer is
0.0052 °C–1 and the resistance of the thermometer is 100 at 20°C.
Assume the connecting leads are at 20°C.
Homework Equations
.[/B]
Rt = R0(1 + at)
R1RT = R2RS
R = pL/A = Resistance = (Resistivity) x Length of wire / cross-sectional area
A = (pi x d2) / 4
d = squareroot(4A /pi)
The Attempt at a Solution
.[/B]
R0 = Rt /(1 + at)
R0 = 100 /(1 + 0.0052 x 20) = 90.58 ohms
R150 = 90.58 /(1 + 0.0052 x 150) = 50.89 ohms
Fundamental Interval = Rt - R0 = 90.58 - 50.89 = 39.69 ohms = RS
R1RT = R2RS
RT = R2RS / R1 = 150 x 39.69 / 150 = 39.69 ohms
R = pL/A
A = pL/R = (0.0000000168 x 200) / 39.69 = 0.00000336 m2 = 3.36 mm2
d = squareroot(4A /pi) = squareroot(4 x 3.36 / pi) = 4.27mm = 7 swg.
Please let me know if I am in the right direction on this, it's been puzzling me for a few days now!