Mathematica How to draw integral with mathematica

[EliasS]

Hello,
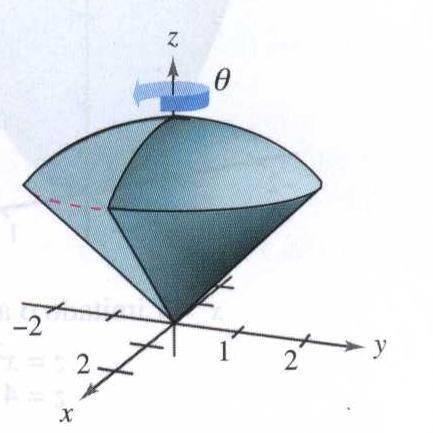
is there a way to draw the volume of a triple integral?, and in different ways?(rectangular, cylindrical and sphere coordinates)
for example if the integral is

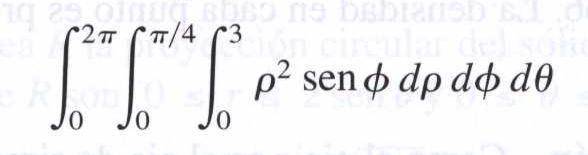
what I want is to draw directly with the above formula

I have been struggling all day with this, because if for example I use something like Plot3D[Integrate[x... it will first solve the integral, which will become a constant and then draw that constant

Also there must be a way because in the calculus book I'm studying, in many exercises it ask you to draw the volume of the problem with a software tool

Thank you, I really need this

 

[Dale]

What you want to plot here is not the integrand nor the integral, what you want to plot is the limits of integration. I would use ParametricPlot3D or RegionPlot3D, but you will have to transform from spherical coordinates to Cartesian coordinates either way.

 

[EliasS]

Thank you DaleSpam, now I can draw integrals in rectangular coordinates, for example, the integral

RegionPlot3D[-2 < x < 2 && -\[Sqrt](4 - x^2) < y < \[Sqrt](4 - x^2) && x^2 + y^2 < z < 4, {x, -2, 2}, {y, -2, 2}, {z, 0, 5}, PlotPoints -> 50, Mesh -> True, AxesLabel -> Automatic]
will draw

but for spherical coordinates, I found the sentence SphericalPlot3D, which for example with
SphericalPlot3D[{1}, {\[Phi], 0, Pi/4}, {\[Theta], 0, 2 Pi}]
will draw

but I doesn't draw the cone underneath the sphere, my question is, is there a way to do that?

I thought something like saying to mathematica "draw me rho from 0 to 1 continuously ", and it would draw

, but the cone being solid

thank you

 

[Hepth]

I'd use region plot and just use spherical coordinates. Its slower, and requires tweaking due to the angles but :

r = Sqrt[x^2 + y^2 + z^2];
\[Phi] = ArcTan[y/Abs[x]];
\[Theta] = ArcCos[Abs[z]/Sqrt[x^2 + y^2 + z^2]];
RegionPlot3D[
0 < r <= 3 && 0 < Abs[\[Theta]] < \[Pi]/4, {x, -5, 5}, {y, -5,
5}, {z, 0, 5}, PlotPoints -> 60, Mesh -> True,
AxesLabel -> Automatic, PlotRange -> {{-3, 3}, {-3, 3}, {-1, 5}}]

http://en.wikipedia.org/wiki/Spherical_coordinatesSame for cylindrical. You just have to do a coordinate conversion back to cartesian.