How to find the inductance of this circuit

[MissP.25_5]

I got stuck doing this question. Please correct my mistakes and help me out.

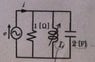
1. The angular frequency ω is FIXED to 2 [rad/s] whereas the inductance L is changeable. When L=1/8, resonance occurs in the circuit and the magnitude of current i reaches its minimum value. From this state, L is increased to L=L1 and current i becomes √2 of its minimum value. Find L1.

2. The inductance L is fixed to L1 (found in question 1) while ω is variable. When ω= ω0, the magnitude of current i reaches its minimum value. Find ω0.

 

[gneill]

Check your value for ZL. (At resonance you'd expect the inductive and capacitive impedances to be complex conjugates (i.e., they'll cancel if added)).

Since you're looking for a ratio in part 2, you might as well just choose a convenient value for the voltage source. Letting e = 1 [V] looks promising. What's the current I_o at resonance then?

 

[MissP.25_5]

Check your value for ZL. (At resonance you'd expect the inductive and capacitive impedances to be complex conjugates (i.e., they'll cancel if added)).

Since you're looking for a ratio in part 2, you might as well just choose a convenient value for the voltage source. Letting e = 1 [V] looks promising. What's the current I_o at resonance then?

At resonance, the ZL+ZC is 0 in a series circuit. Is it the same as in this parallell circuit?

 

[gneill]

At resonance, the ZL+ZC is 0 in a series circuit. Is it the same as in this parallell circuit?

You'll find that they also cancel when added in parallel. Try it:
$$Z = \frac{1}{\frac{1}{R} + \frac{1}{ZL} + \frac{1}{ZC}}$$
and at resonance ZC = -ZL ... so ...

 

[MissP.25_5]

You'll find that they also cancel when added in parallel. Try it:
$$Z = \frac{1}{\frac{1}{R} + \frac{1}{ZL} + \frac{1}{ZC}}$$
and at resonance ZC = -ZL ... so ...

Is the circuit still in resonant state when L is is increased to L1?I guess not, though, because then L=1/8 and it's back to square 1.

 

[MissP.25_5]

So in a parallel circuit, the total impedance of ZL and ZC is indeed 0. But when L increases to L1, the circuit is no more at resonance, isn't it? Am I doing this right? The method I am using seems to be too long, and I think it's impossible to get it.

 

[gneill]

So in a parallel circuit, the total impedance of ZL and ZC is indeed 0. But when L increases to L1, the circuit is no more at resonance, isn't it? Am I doing this right? The method I am using seems to be too long, and I think it's impossible to get it.

I see that the math got a bit hairy pretty quickly. So if I might suggest... rather than going for the total impedance, you can go for the total current right away.

This is a parallel circuit so every branch has the same potential difference and the branch currents sum. Choosing a suitable potential for the voltage source, say 1 V at 2 rad/sec, will make summing the currents a piece of cake.

 

[MissP.25_5]

I see that the math got a bit hairy pretty quickly. So if I might suggest... rather than going for the total impedance, you can go for the total current right away.

This is a parallel circuit so every branch has the same potential difference and the branch currents sum. Choosing a suitable potential for the voltage source, say 1 V at 2 rad/sec, will make summing the currents a piece of cake.

When finding the sum of the currents, should I take the magnitudes of iC and iL or just leave them be as complex terms? I'm still not used to when to use magnitudes, can you give me some tips?

 

[gneill]

When finding the sum of the currents, should I take the magnitudes of iC and iL or just leave them be as complex terms? I'm still not used to when to use magnitudes, can you give me some tips?

Almost always you want to keep everything in complex form. An exception is when you are calculating power, but even then you can do that in complex form as well (calculating the complex power and then extracting the effective power as the real term). This avoids having to remember how to deal with power factors applied to the product of the voltage and current magnitudes

 

[MissP.25_5]

Almost always you want to keep everything in complex form. An exception is when you are calculating power, but even then you can do that in complex form as well (calculating the complex power and then extracting the effective power as the real term). This avoids having to remember how to deal with power factors applied to the product of the voltage and current magnitudes

Ok, I'm done with the calculation. I got L1=1/8, this cannot be right ? I used your method of using current and then I just equate the terms with its real and imaginary coefficients. I'm not sure if I did it right, though.

 

[gneill]

Ok, I'm done with the calculation. Is L1=1/8 ? I used your method of using current and then I just equate the terms with its real and imaginary coefficients. I'm not sure if I did it right, though.

You can sum the currents as before, but this time it's the magnitude of the current you're looking for. So the magnitude rises to √2 x the initial current. I'm not seeing 1/8 for L1.

 

[MissP.25_5]

You can sum the currents as before, but this time it's the magnitude of the current you're looking for. So the magnitude rises to √2 x the initial current. I'm not seeing 1/8 for L1.

Of course, because L=1/8 is when the circuit is at resonance. I forgot.

 

[MissP.25_5]

You can sum the currents as before, but this time it's the magnitude of the current you're looking for. So the magnitude rises to √2 x the initial current. I'm not seeing 1/8 for L1.

Ok, I fixed it. L=1/6, right?

 

[gneill]

Ok, I fixed it. L=1/6, right?

Yes!

 

[MissP.25_5]

Yes!

Now, to find ω0, do I have to use the same method too?

 

[gneill]

Now, to find ω0, do I have to use the same method too?

This time you have all the component values, and in particular, the inductance and capacitance. At resonance, what condition holds for those two components? (it was mentioned earlier).

 

[MissP.25_5]

This time you have all the component values, and in particular, the inductance and capacitance. At resonance, what condition holds for those two components? (it was mentioned earlier).

ZL=-ZC is the condition. But, how do you know that it's at resonance? It only says that the current reaches its minimum value. But I used current to find omega and got the answer. Look...

 

[gneill]

ZL=-ZC is the condition. But, how do you know that it's at resonance? It only says that the current reaches its minimum value. But I used current to find omega and got the answer. Look...

The only time the current can reach its minimum value is when the circuit is at resonance. That is, the capacitor and inductor impedances mutually cancel and they "disappear" from the circuit. Minimum current for a parallel RLC circuit occurs at resonance.

Knowing that, you know that XL = XC; the reactances are equal. (Reactance is magnitude of the impedance)

So just equate the reactances of the two reactive components.

The result you found is correct, even if you pursued a longer path to it