- #1
sergiohjm
- 2
- 1
Thread moved from the technical forums to the schoolwork forums
- Homework Statement
- .
- Relevant Equations
- .
Hello everyone,
I need to solve a problem applying symmetry and superposition theorem but the problem is that the circuit is almost symetrical but has little differences in both sides (the source in the left side and the unknown impedance in the right side). I couldn't solve the problem using only Kirchoff's laws.
An example would be:
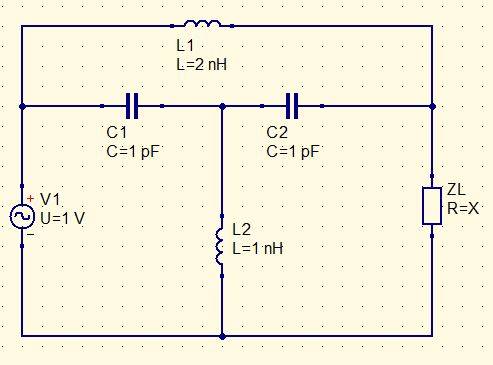
I know I can separate L1 in two inductances in series and L2 in two inductances in parallel but I don't know what to do with ZL.
The problem asks to determine the potential difference in ZL and the value of ZL when the potential in L2 is 0.
I would thank any help no matter how small
Thanks in advance
I need to solve a problem applying symmetry and superposition theorem but the problem is that the circuit is almost symetrical but has little differences in both sides (the source in the left side and the unknown impedance in the right side). I couldn't solve the problem using only Kirchoff's laws.
An example would be:
I know I can separate L1 in two inductances in series and L2 in two inductances in parallel but I don't know what to do with ZL.
The problem asks to determine the potential difference in ZL and the value of ZL when the potential in L2 is 0.
I would thank any help no matter how small
Thanks in advance