How to Generate Initial Conditions for Modeling Galactic Spiral Arms?

[fab13]

I need to generate initial conditions for modeling galactic spiral arms.

I start with the following polar equation:

rho = a. / (log (b * tanh (theta / (2 * n))) with a, b ​​and n are parameters to choose from.

to give a thickness along the curve for the generated points, I did the following things:

- I generate points in a rectangle of width hx and height hy.
- I divided the polar curve in several segments delta(theta) then I calculate the value of the tangent vector to the polar curve at each point of the segments
- I calculate the angle between the tangent vector and the vector ex (canonical basis vector ex)
- I apply the rotation matrix with this angle to the set of points generated.
- I applies a translation of the new points with the angle theta of the considered point (the point on the curve corresponding to the segment in question)

Note that I managed to reduce the hy thickness gradually (as theta increases).

but now, I can't produce a thickness for small theta, i.e reproduce the bar in the middle that joins the two spiral arms. You can see the result on the following figure :

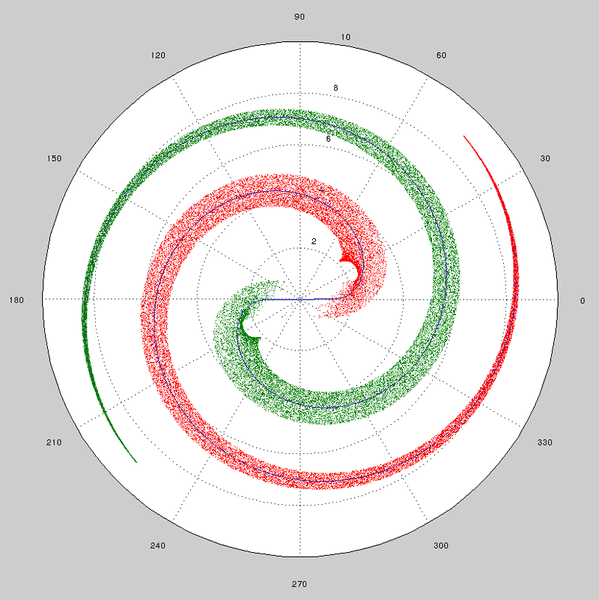
You can see that there are artifacts on the figure for small theta.

Here's the original MATLAB source for this figure :

function test_arms

% Total number of particles
num_particles=25600;
% Number of segments
num_seg=800;
% Number of particules per segment
num_part_seg=num_particles/(2*num_seg);

% Parameters for curbe
a1=10;
b1=0.5;
n1=4;

% Theta max
theta_max=2.25*pi;
% Width along curve
width=2;
% Hx width
hx=theta_max/num_seg;
% Hy width : decreasing with theta
hy=width-width.*(1:num_seg)/num_seg;
% Theta array
t=0:hx:theta_max-hx;
% Function values
f1=a1./(log(b1*tanh(2*pi*t/(theta_max*(2*n1)))));
% Derivates
f11_prim=diff(f1)./diff(t);
f12_prim=diff(-f1)./diff(t);

f11_prim(num_seg)=0;
f12_prim(num_seg)=0;
% Tangent vector coordinates
x_dom=(f11_prim-f1.*sin(t));
y_dom=(f12_prim+f1.*cos(t));
% Angle value with ex
alpha11=-atan(y_dom./x_dom);
alpha12=atan(-y_dom./x_dom);


for i=1:num_seg
    
    % Random box coordinates for f1
    x11_first=hx*(rand(num_part_seg,1)-0.5);    
    y11_first=hy(i)*(rand(num_part_seg,1)-0.5);
    
    % Rotation matrix + translation
    x11((i-1)*num_part_seg+1:i*num_part_seg)=(x11_first*cos(alpha11(i))+y11_first*sin(alpha11(i)))+f1(i)*cos(t(i));
    y11((i-1)*num_part_seg+1:i*num_part_seg)=(-x11_first*sin(alpha11(i))+y11_first*cos(alpha11(i)))+f1(i)*sin(t(i));

    % Random box coordinates for -f1
    x12_first=hx*(rand(num_part_seg,1));    
    y12_first=hy(i)*(rand(num_part_seg,1)-0.5);

    % Rotation matrix + translation
    x12((i-1)*num_part_seg+1:i*num_part_seg)=(x12_first*cos(alpha12(i))+y12_first*sin(alpha12(i)))-f1(i)*cos(t(i));
    y12((i-1)*num_part_seg+1:i*num_part_seg)=(-x12_first*sin(alpha12(i))+y12_first*cos(alpha12(i)))-f1(i)*sin(t(i));

end    


figure(1);
polar(t,f1);
hold on;
polar(t,-f1);
hold on;
scatter(x11,y11,1);
hold on;
scatter(x12,y12,1);

end

I thought this issue comes from the subsampling of my segments for little theta, so I tried to fix that with this modified source :

function test_arms_2

% Total number of particles
num_particles=50000;
% Number of segments
num_seg=5000;
% Number of particules per segment
num_part_seg=num_particles/(2*num_seg);

% Parameters for curbe
a1=10;
b1=0.5;
n1=4;

%num_seg of bar
num_seg_bar=2000;
num_seg_spiral=num_seg-num_seg_bar;

% Theta min
theta_min=0.25*pi;
% Theta max
theta_max=2.25*pi;
% Width along curve
width=2;
% Hx bar width
hx_bar=theta_min/num_seg_bar;
% Hx spiral width
hx_spiral=(theta_max-theta_min)/num_seg_spiral;
% Hy width : decreasing with theta
hy=width-width.*(1:num_seg)/num_seg;
% Theta array
t=[linspace(0,theta_min,num_seg_bar) linspace(theta_min,theta_max,num_seg_spiral)];
hx(1:num_seg_bar)=hx_bar;
hx(num_seg_bar+1:num_seg)=hx_spiral;
% Function values
f1=a1./(log(b1*tanh(2*pi*t/(theta_max*(2*n1)))));
% Derivates
f11_prim=diff(f1)./diff(t);
f12_prim=diff(-f1)./diff(t);

f11_prim(num_seg)=0;
f12_prim(num_seg)=0;
% Tangent vector coordinates
x_dom=(f11_prim-f1.*sin(t));
y_dom=(f12_prim+f1.*cos(t));
% Angle value with ex
alpha11=-atan(y_dom./x_dom);
alpha12=atan(-y_dom./x_dom);


for i=1:num_seg
    
    % Random box coordinates for f1
    x11_first=hx(i).*(rand(num_part_seg,1)-0.5);    
    y11_first=hy(i)*(rand(num_part_seg,1)-0.5);
    
    % Rotation matrix + translation
    x11((i-1)*num_part_seg+1:i*num_part_seg)=(x11_first*cos(alpha11(i))+y11_first*sin(alpha11(i)))+f1(i)*cos(t(i));
    y11((i-1)*num_part_seg+1:i*num_part_seg)=(-x11_first*sin(alpha11(i))+y11_first*cos(alpha11(i)))+f1(i)*sin(t(i));

    % Random box coordinates for -f1
    x12_first=hx(i).*(rand(num_part_seg,1));    
    y12_first=hy(i)*(rand(num_part_seg,1)-0.5);

    % Rotation matrix + translation
    x12((i-1)*num_part_seg+1:i*num_part_seg)=(x12_first*cos(alpha12(i))+y12_first*sin(alpha12(i)))-f1(i)*cos(t(i));
    y12((i-1)*num_part_seg+1:i*num_part_seg)=(-x12_first*sin(alpha12(i))+y12_first*cos(alpha12(i)))-f1(i)*sin(t(i));

end    


figure(1);
polar(t,f1);
hold on;
polar(t,-f1);
hold on;
scatter(x11,y11,1);
hold on;
scatter(x12,y12,1);

end

Anyone could see how to reproduce this central bar... ?

Thanks

 

[mfb]

Where is the point in those rotated squares (I think their overlap generates the dense regions, and probably some other issues)? You can use coordinates in a circle, then you don't need those rotations. Just make sure that your sampling of the curve is much denser than the width of the curve there. To improve this: the outer regions can use circles with only a few points inside.
That simplifies the code significantly, it gets rid some strange features and it is easier to change things.

Concerning your main issue:
The central bar is certainly a problem of your theta coordinate - the range between 0 to .1 pi gives the whole range where your points look strange (including the overdensity) and the central bar is just between 0 and 0.001 pi.

Possible ideas I see:
(1) sample in r instead of theta. It is easy to convert your function to theta(r).
(2) take curve length between your theta-steps into account to get the same curve length per step. Probably easier combined with (1).
(3) treat the curve as graph, use those points and forget the underlying polar function.
(4) add the central bar manually. Probably a very ugly solution.