- #1
Richard_Steele
- 53
- 3
I am just starting a course about machine learning and I don't know how to interpret the cost function.
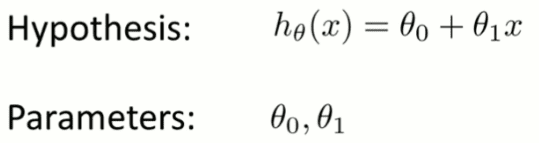
When the teacher draws the straight line in the x and y coordinates, it looks like:
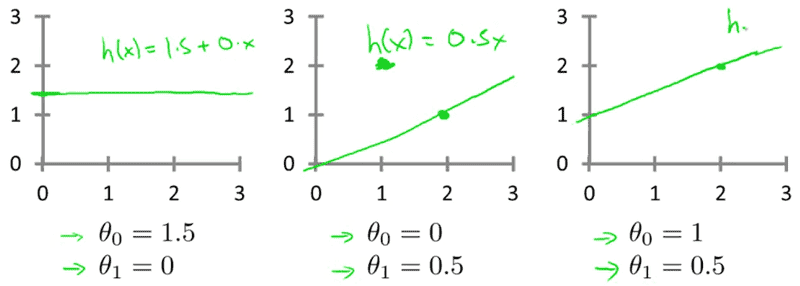
I see that theta zero is the start of the straight line (in the left side) in the Y coordinate.
The question is related about what theta one modifies? theta one modifies the inclination?
When the teacher draws the straight line in the x and y coordinates, it looks like:
I see that theta zero is the start of the straight line (in the left side) in the Y coordinate.
The question is related about what theta one modifies? theta one modifies the inclination?