How to Prove \(\text{vol}_n (B) = \text{vol}_n (B') + \text{vol}_n (B'')\)?

[Math Amateur]

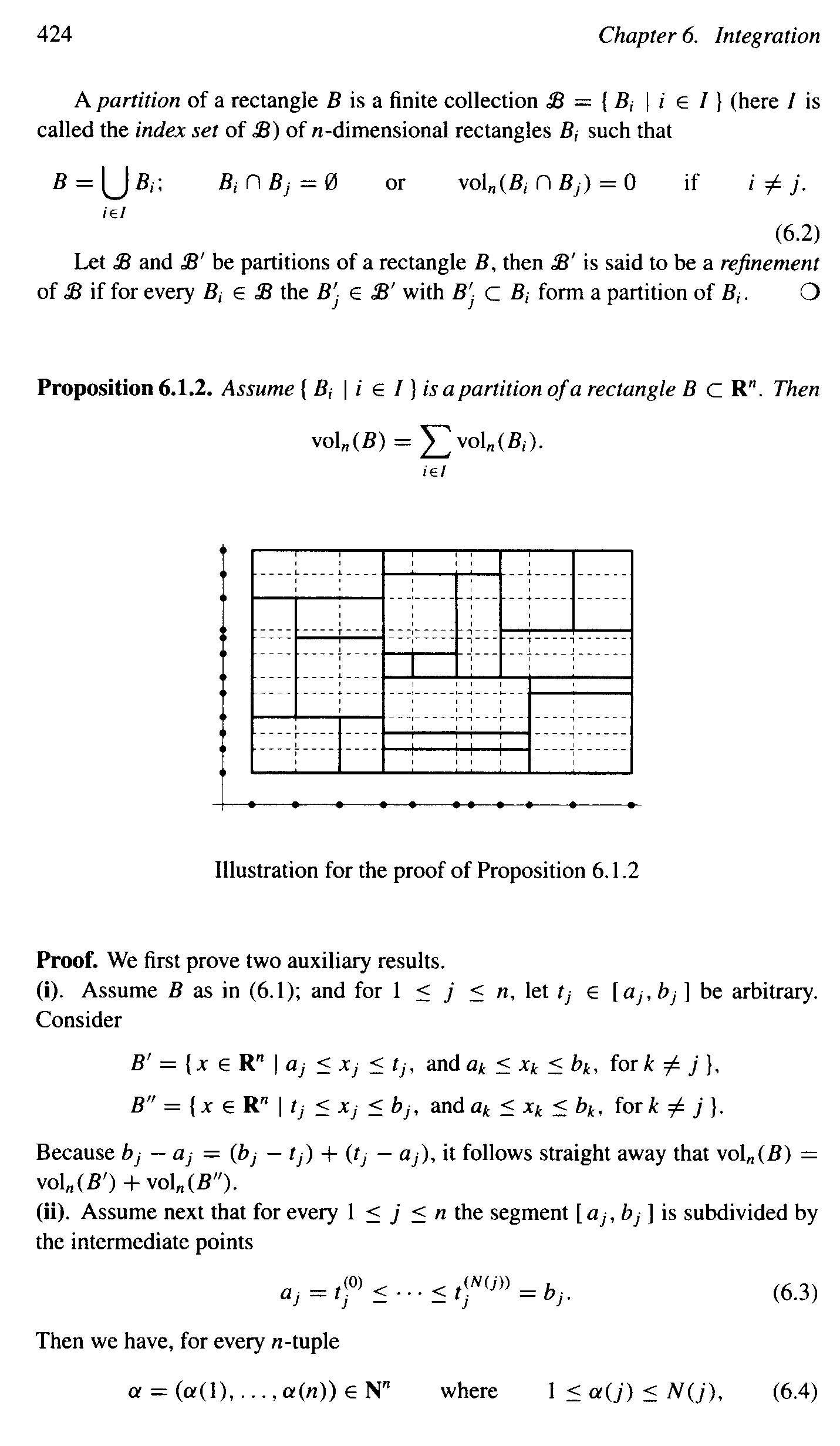
I am reading Multidimensional Real Analysis II (Integration) by J.J. Duistermaat and J.A.C. Kolk ... and am focused on Chapter 6: Integration ...

I need some help with the proof of Proposition 6.1.2 ... and for this post I will focus on the first auxiliary result ... see (i) ... at the start of the proof ...Near the start of the proof of Proposition 6.1.2 D&K state that :

" ... ... Because b_j - a_j = (b_j - t_j) + (t_j - a_j), it follows straight away that :

[math] \text{ vol}_n (B) = \text{ vol}_n (B') + \text{ vol}_n (B'') [/math]Readers of this post only need to read the very first part of the proof of Proposition 1 (see scanned text below) ... BUT ... I am providing a full text of the proof together with preliminary definitions so readers can get the context and meaning of the overall proof ... but, as I have said, it is not necessary for readers to read any more than the very first few lines of the proof.
Can someone please help me to rigorously prove that [math] \text{ vol}_n (B) = \text{ vol}_n (B') + \text{ vol}_n (B'') [/math] ...Hope someone can help ...

Help will be much appreciated ...

PeterThe proof of Proposition 6.1.2 together with preliminary notes and definitions reads as follows:

Hope that helps,

Peter

 

[Euge]

Hi Peter,

By definition of volume, $$\text{vol}_n(B') = (t_j - a_j)\prod_{k \neq j} (b_k - a_k)\quad \text{and}\quad \text{vol}_n(B'') = (b_j - a_j) \prod_{k \neq j} (b_k - a_k)$$
Hence the sum $$\text{vol}_n(B') + \text{vol}_n(B) = [(t_j - a_j) + (b_j - a_j)] \prod_{k \neq j} (b_k - a_k) = (b_j - a_j)\prod_{k \neq j} (b_k - a_k) = \prod_k (b_k - a_k) = \text{vol}_n(B)$$ as desired.

 

[soloenergy]

Preliminary notes and definitions:

Let B = [a_1, b_1] \times [a_2, b_2] \times ... \times [a_n, b_n] be a closed n-dimensional rectangle in \mathbb{R}^n. We define the volume of B as:

\text{vol}_n (B) = (b_1 - a_1)(b_2 - a_2) ... (b_n - a_n)

Now, let t_j \in [a_j, b_j] for j = 1, 2, ..., n. We define the rectangles B' = [a_1, t_1] \times [a_2, t_2] \times ... \times [a_n, t_n] and B'' = [t_1, b_1] \times [t_2, b_2] \times ... \times [t_n, b_n].

Proposition 6.1.2: Let B, B', B'' be as defined above. Then, \text{ vol}_n (B) = \text{ vol}_n (B') + \text{ vol}_n (B'').