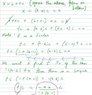How to Solve a Vector Equation with Doubts on the Solution?

[PcumP_Ravenclaw]

I have some doubts about the solution to $x + (x \cdot a)c = b$ according to the first attachment, (Alan F. Beardon, Algebra and geometry)? λ = 1 and μ =1

He says that we should view the above equation as a line $x + t*c = b$ then substitute this x back into $x + (x \cdot a)c = b$ but t also has x in it? As $x + t*c = b$ comes from $x + (x \cdot a)c = b$ how can we put it back into the original equation as above?

Next, I made the substitution in the second attachment. Please explain why t is all the real numbers as solution when $a \cdot b = 0$ AND $1 + a \cdot c = 0$? $\frac{0}{0}$ is undefined right? is that why t can be any value?

 

[Svein]

x+(x⋅a)c=b

So scalar multiply this equation with a. This will give you a solution for x⋅a and then for x.

 

[PcumP_Ravenclaw]

So scalar multiply this equation with a. This will give you a solution for x⋅a and then for x.

$x \cdot a +(x \cdot a)(c \cdot a) = (b \cdot a)$

factorising $x \cdot a$ gives $(x \cdot a)(1 + (c \cdot a)) = (b \cdot a)$

$(x \cdot a) = \frac{(b \cdot a)}{(1 + (c \cdot a))}$

say RHS = the scalar m then

$x_1 a_1 + x_2 a_2 + x_3 a_3 = m$ now how to find x1, x2 & x3?

 

[Svein]

now how to find x1, x2 & x3?

You have just computed x⋅a. Your original equation says x+(x⋅a)c=b. I assume that b and c are given. Solve for x