Md. Abde Mannaf
- 20
- 1
Homework Statement
Homework Equations
The Attempt at a Solution
here is i am still stuck.
The discussion revolves around solving an integral using the Leibniz Rule, specifically the expression $$\frac{d}{dx} \int_{a(x)}^{b(x)} f(t) dt = f(b(x)) b'(x) - f(a(x)) a'(x)$$. Participants express confusion regarding the problem statement and suggest using variable substitutions, such as ##u = \tan(x/2)## and ##u = \cos(x)##, to simplify the integral. The conversation highlights the challenges of integrating functions like $$\int \frac{1}{1+\alpha \cos(x)} dx$$ and recommends using tools like Wolfram Alpha for assistance. The consensus is that while the Leibniz Rule is applicable, the integral remains complex and requires careful manipulation.
PREREQUISITESStudents of calculus, mathematicians, and anyone tackling complex integrals using the Leibniz Rule and trigonometric substitutions.
Don't use substitution, use Leibniz rule with α as the second variable.
Md. Abde Mannaf said:i know the Leibniz's rule. i solve many mathematical term . bt i cann't solve this math with Leibniz rule. i am still stuck
here. here limit is constant so 2nd and 3rd term will be zero.
See this, example 3.Zondrina said:if you are intending to use Leibniz rule. I for one have never seen an In\text{In} function before.
You can even cheat :) using wolframalpha.com.Md. Abde Mannaf said:Homework Statement
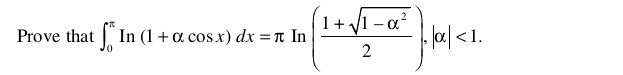
Homework Equations
The Attempt at a Solution
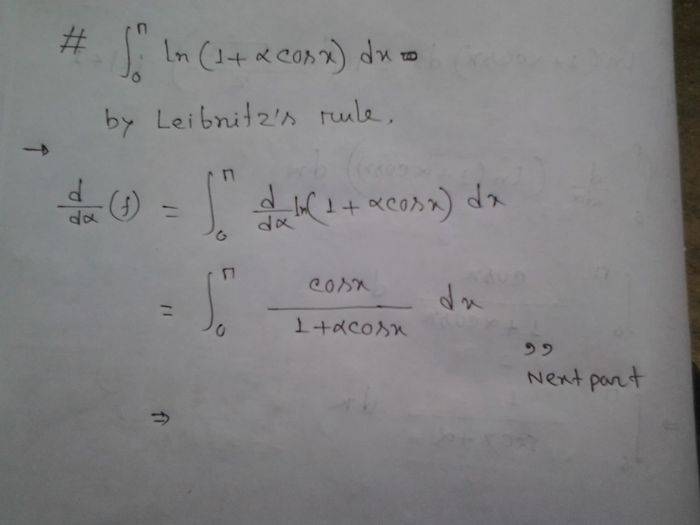
here is i am still stuck.
Zondrina said:I believe there are quite a few typos in the problem statement if you are intending to use Leibniz rule. I for one have never seen an ##\text{In}## function before.
The Leibniz rule in one dimension would be:
$$\frac{d}{dx} \int_{a(x)}^{b(x)} f(t) dt = f(b(x)) b'(x) - f(a(x)) a'(x)$$
EDIT: It would be more appropriate to call this the fundamental theorem.
Does no one read my posts :-)ehild said:You can even cheat :) using wolframalpha.com.
You can write your integral for ##f'(\alpha)## as ##\int_0^{\pi/2} + \int_{\pi/2}^{\pi}##, then change variables to ##x \leftarrow \pi -x## in the second integral, to getMd. Abde Mannaf said:i could not solve this math above analysis . i am trying to my best. but i am fail every time. and again try...
please see this and give me more idea to solve
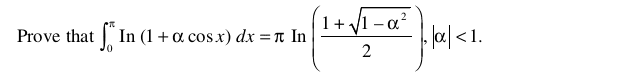
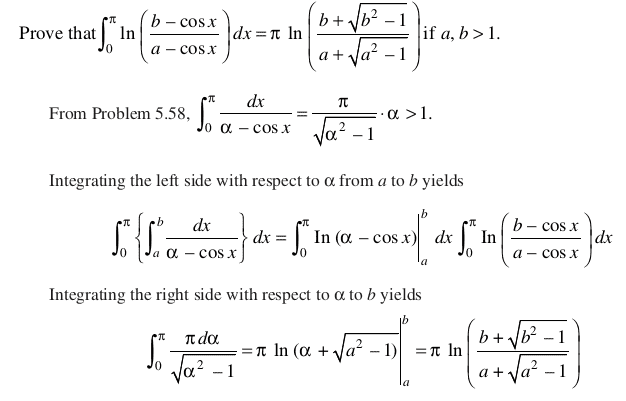
##\int \frac{1}{1+\alpha cos(x)} dx## is not that nasty.certainly said:Now let's do that daunting looking integral. Like I said before, this is a good problem.
First write ##\int_0^{\pi} \frac{1}{\alpha}-\frac{1}{(\alpha)(1+\alpha cos(x))} dx## for the original integral.
However ##\int \frac{1}{1+\alpha cos(x)} dx## itself is not nice, in-fact it's pretty nasty.
Yeah, your right. I didn't actually do the integral, I only saw the answer and thought, this might take some time.ehild said:##\int \frac{1}{1+\alpha cos(x)} dx## is not that nasty.
Use the identity ##\cos(x)=\frac{1-\tan^2(x/2)}{1+\tan^2(x/2)}##. Substitute u=tan(x/2), x=2arctan(u), ##dx=\frac{2}{1+u^2}du##. The integration limits become 0-->infinite.