How to study feedback? Which branch of Mathematics does it?

[jonjacson]

Hello,

I want to study a system, and I have realized that all variables in it are dependent. There is no independent variable. So everytime you modify the input, you get an output but at the same time that output modifies the input itself, there is an important feedback. So the system apparently is evolving searching a kind of equilibrium but it does it in several steps and I find it difficult to "isolate" one variable, or analyze what is the relationship between variables since they are affected by the rest of the system.

I will try to put an example, hopefully it will show the main characteristics I am talking about.

In the atmosphere if there is a raise in the amount of energy that arrives from the sun, the temperature raises. But that changes the amount of water the air can contain, and that modifies the amount of radiation that the atmosphere absorbs which is the factor we started analyzing.

My question is, What is the best mathematical tool to understand systems where feedback between variables is key?

-----

Another example:

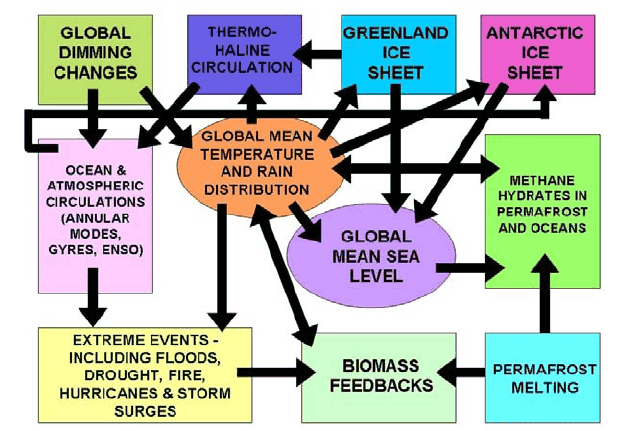
Would you use differential equations? Variational calculus?

 

[1MileCrash]

Is this not Chaos theory, essentially?

 

[AlephZero]

It has nothing to do with Chaos theory unless the system happens to be chaotic, and many systems as complex as the OP's picture are not.

Differential equations, signal processing (analog and digital), and control systems (stability analysis, etc) would be good topics to start learning. You may need some probability theory as well.

 

[HallsofIvy]

With 'feed back', this would be "non-linear differential equations" or, more generally, "non-linear analysis".

 

[SteamKing]

It's not 'chaos theory' you are looking for, but 'control theory' which deals with inputs to dynamical systems and the resulting feedback:

http://en.wikipedia.org/wiki/Control_theory

It's not a branch of pure mathematics which deals with feedback, but a blend of math and engineering, an inter-disciplinary effort.

 

[jonjacson]

Is this not Chaos theory, essentially?

Well, I don't know if the system is chaotic or not. It is complex for sure. I guess a small change could have a big impact on other variables but this is only guessing.

With 'feed back', this would be "non-linear differential equations" or, more generally, "non-linear analysis".

Thanks, I will try to learn that.

It has nothing to do with Chaos theory unless the system happens to be chaotic, and many systems as complex as the OP's picture are not.

Differential equations, signal processing (analog and digital), and control systems (stability analysis, etc) would be good topics to start learning. You may need some probability theory as well.

Thank you very much. That looks very interesting.

 

[jonjacson]

It's not 'chaos theory' you are looking for, but 'control theory' which deals with inputs to dynamical systems and the resulting feedback:

http://en.wikipedia.org/wiki/Control_theory

It's not a branch of pure mathematics which deals with feedback, but a blend of math and engineering, an inter-disciplinary effort.

I have a question about this, Can people using control theory do experiments?

I mean, in mechanics you could go to a laboratory and analyze a pendulum. But the problem is that I can't do any experiment, it is like the atmosphere, you can't stop it and analyze any specific variable.

Everything is mixed together and evolving constantly in time. The same problem you have in astrophysics, you can't stop the universe nor isolate a galaxy, I can just watch everything mixed and changing in time.

Does that matter for control theory?

 

[AlephZero]

I have a question about this, Can people using control theory do experiments?

Sure. For example one of the "standard" experiments is to design a system that will balance an inverted pendulum on a moving cart. Making a computer simulation would probably be a good thing to do first. Then build the real world system and get it working!

https://www.youtube.com/watch?v=AuAZ5zOP0yQ

You can't easily experiment with a system like the Earth's atmosphere, but you can collect data and use it to estimate the parameters that control how the system behaves. That procedure is called "system identification".

 

[jonjacson]

Sure. For example one of the "standard" experiments is to design a system that will balance an inverted pendulum on a moving cart. Making a computer simulation would probably be a good thing to do first. Then build the real world system and get it working!

https://www.youtube.com/watch?v=AuAZ5zOP0yQ

You can't easily experiment with a system like the Earth's atmosphere, but you can collect data and use it to estimate the parameters that control how the system behaves. That procedure is called "system identification".

That looks exactly what I was looking for. Thanks.