- #1
IsaiahvH
Hi,
I am a student in the Netherlands, currently 17 years old and at the end of my 'middelbare school', meaning that next year I'll be a bachelor student at a university.
I am doing an extended essay/research thing that is custom you do in your last year, with a friend of mine.
We picked the topic of antimatter and we want to look at the energy values of electrons.
Our teacher suggested we would create a model based on Schrödinger's Equation in MATLAB.
I have created such a model, 1D, but I don't fully understand the equation, which seems rather abstract to me, and have no idea how to create a 2D version and eventually a 3D version. Our teacher's advice? Ask you guys (or girls, of course).
My first question: What does Schrödinger's equation mean?
This is the least important of my questions; I understand what it provides (particle probability) and how to construct a model out of it, but it feels wrong to work with something I don't fully understand. Examples found on the internet are difficult to comprehend for me, but nevertheless I'd hoped someone could shed some light on this.
The formula we use, is this one.
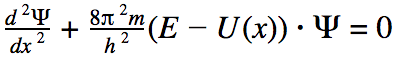
It's a somewhat rewritten version from a schoolbook.
This has been turned into the following code.
Of course, all variables are given a start value beforehand, but basically this is the piece that concerns the formula. The point is, this piece basically draws the wave function (or Ψ, if I'm correct) based on the given E, the energy value. The graph is also dependant on a given situation, described in fu g, which is in this example set to C (= 1) * x^2. The graph results in the wave function (being the square of the probability function?), which should, as fu gets incredibly high, get smaller and smaller and have an asymptote to zero. However, our E is not entirely precise, resulting in the graph only staying horizontal for a while, before having an asymptote either up or down. The more accurate the given E is (more decimals), the longer it 'stays' horizontal (before going up or down, but this can be ignored).
The perfect E is found on this idea;
The end of the graph holds information on where the nearest perfect E value is. If it's pointing up, the perfect E is actually above the given one right now. Based on this principle, our code determines the best decimal and then moves on to the next decimals, determining the E up until 15 decimals, and indeed, the more accurate decimals, the longer our graph stays flat.
This is my second question: Can I use this idea that the tail of the graph always points to the nearest energy value? It definitely seems to work, and I can calculate seemingly okay E-values, and the graph gets flatter on the end using this idea. I also got an alternative version where the graph is given points on how long it's flat, and based on that principle it finds the perfect E-value, but I'd prefer this one.
Another piece surrounding these basically leads to the next E-value, as in Schrödinger's Equation you got these multiple E-values corresponding with the fixed energy states the particle (electron) can be in.
All this together results in the following graph
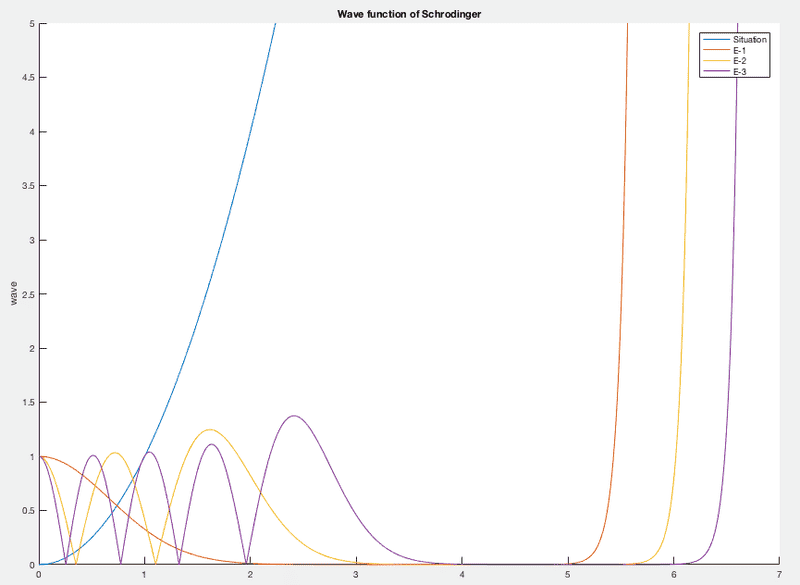
The blue line represents the situation, x^2.
The orange one is the first energy state, the yellow one the second and the purple one the third (there are more), with the corresponding energy values of
E-1 = 0.4471758673234
E-2 = 4.0247949984073
E-3 = 7.6024556510729
I haven't got the slightest idea if this is correct, but hell, it seems okay?
(That's what my teacher said as well.)
This all leads to my third and main question: How do I expand this to a 2D (and eventually) a 3D environment to fully create a model of Hydrogen?
Is my current code usable (if correct at all), and expandable to a 2D environment? What needs to be done? Is it not usable at all, is it completely incorrect?
____________________________________________________________________
I would massively appreciate any help, even if not directly an answer to one of my questions.
I hope there's someone who knows about this and would be willing to help.
I did my best to explain my current idea, questions and model as well as possible, but I can easily imagine it's insufficient. I have had no experience beforehand with either this formula, or MATLAB.
Any further explanation I'd be happy to provide!
Also, if necessary, my code can be found https://drive.google.com/open?id=0B5_0h9k46DFuQXlGUUM3WmxhNEU.
Basically, if the Supporting Functions folder is included, quantumrun.m can be run without problems (supposedly). The code I described, which calculates the graph, can be found in calculate_fy.m
Thanks to anyone in advance!
Kind regards,
Isaiah van Hunen
I am a student in the Netherlands, currently 17 years old and at the end of my 'middelbare school', meaning that next year I'll be a bachelor student at a university.
I am doing an extended essay/research thing that is custom you do in your last year, with a friend of mine.
We picked the topic of antimatter and we want to look at the energy values of electrons.
Our teacher suggested we would create a model based on Schrödinger's Equation in MATLAB.
I have created such a model, 1D, but I don't fully understand the equation, which seems rather abstract to me, and have no idea how to create a 2D version and eventually a 3D version. Our teacher's advice? Ask you guys (or girls, of course).
My first question: What does Schrödinger's equation mean?
This is the least important of my questions; I understand what it provides (particle probability) and how to construct a model out of it, but it feels wrong to work with something I don't fully understand. Examples found on the internet are difficult to comprehend for me, but nevertheless I'd hoped someone could shed some light on this.
The formula we use, is this one.
It's a somewhat rewritten version from a schoolbook.
This has been turned into the following code.
Code:
for x = 0:dx:max
fu(z) = C * x.^2;
curve = -1 * massfactor * (E-fu(z)) * wave;
slope = slope + curv * dx;
d_wave = slope * dx;
wave = wave + d_wave;
fy(z) = wave;
z = z + 1;
endx is the distance in the set dimension (1D) of the situation.
C is not explained in our book
Curve refers to the current curve (our book is not clearer)
Massfactor is the 8*pi^2*m/h^2 part, bundled together
Slope is the current slope of the graph
Dx is the delta x
D_wave is the delta wave
Wave is the square of the probability function, also Ψ, if I'm correct
C is not explained in our book
Curve refers to the current curve (our book is not clearer)
Massfactor is the 8*pi^2*m/h^2 part, bundled together
Slope is the current slope of the graph
Dx is the delta x
D_wave is the delta wave
Wave is the square of the probability function, also Ψ, if I'm correct
Of course, all variables are given a start value beforehand, but basically this is the piece that concerns the formula. The point is, this piece basically draws the wave function (or Ψ, if I'm correct) based on the given E, the energy value. The graph is also dependant on a given situation, described in fu g, which is in this example set to C (= 1) * x^2. The graph results in the wave function (being the square of the probability function?), which should, as fu gets incredibly high, get smaller and smaller and have an asymptote to zero. However, our E is not entirely precise, resulting in the graph only staying horizontal for a while, before having an asymptote either up or down. The more accurate the given E is (more decimals), the longer it 'stays' horizontal (before going up or down, but this can be ignored).
The perfect E is found on this idea;
The end of the graph holds information on where the nearest perfect E value is. If it's pointing up, the perfect E is actually above the given one right now. Based on this principle, our code determines the best decimal and then moves on to the next decimals, determining the E up until 15 decimals, and indeed, the more accurate decimals, the longer our graph stays flat.
This is my second question: Can I use this idea that the tail of the graph always points to the nearest energy value? It definitely seems to work, and I can calculate seemingly okay E-values, and the graph gets flatter on the end using this idea. I also got an alternative version where the graph is given points on how long it's flat, and based on that principle it finds the perfect E-value, but I'd prefer this one.
Another piece surrounding these basically leads to the next E-value, as in Schrödinger's Equation you got these multiple E-values corresponding with the fixed energy states the particle (electron) can be in.
All this together results in the following graph
massfactor = 5;
C = 1;
wave = 1;
slope = 0;
C = 1;
wave = 1;
slope = 0;
The blue line represents the situation, x^2.
The orange one is the first energy state, the yellow one the second and the purple one the third (there are more), with the corresponding energy values of
E-1 = 0.4471758673234
E-2 = 4.0247949984073
E-3 = 7.6024556510729
I haven't got the slightest idea if this is correct, but hell, it seems okay?
(That's what my teacher said as well.)
This all leads to my third and main question: How do I expand this to a 2D (and eventually) a 3D environment to fully create a model of Hydrogen?
Is my current code usable (if correct at all), and expandable to a 2D environment? What needs to be done? Is it not usable at all, is it completely incorrect?
____________________________________________________________________
I would massively appreciate any help, even if not directly an answer to one of my questions.
I hope there's someone who knows about this and would be willing to help.
I did my best to explain my current idea, questions and model as well as possible, but I can easily imagine it's insufficient. I have had no experience beforehand with either this formula, or MATLAB.
Any further explanation I'd be happy to provide!
Also, if necessary, my code can be found https://drive.google.com/open?id=0B5_0h9k46DFuQXlGUUM3WmxhNEU.
Basically, if the Supporting Functions folder is included, quantumrun.m can be run without problems (supposedly). The code I described, which calculates the graph, can be found in calculate_fy.m
Thanks to anyone in advance!
Kind regards,
Isaiah van Hunen