I How was the damping scale of the CMB calculated?

[Quarkly]

TL;DR Summary

I ran across this equation in some lecture notes and I'm not able to follow the derivation.

I'm reading through the lecture notes of Wayne Hu regarding the Damping Scale of the CMB. He give the following steps to calculating the damping scale, $k_D$:$$k_D^{-2}=\int \frac{1}{6(1+R)}\left( \frac {16}{15}+ \frac{R^2}{(1+R)}\right)\frac{1}{\dot\tau} d\eta$$Limiting forms:$$\lim\limits_{R \to 0}k_D^{-2}= \frac{1}{6}\frac{16}{15}\int \frac{1}{\dot\tau} d\eta$$
$$\lim\limits_{R \to \infty}k_D^{-2}= \frac{1}{6}\int \frac{1}{\dot\tau} d\eta$$and finally$$k_D=\frac{\sqrt{6}}{\sqrt{\eta \dot\tau^{-1}}}$$I see roughly what he's doing, but my math is rusty. Could anyone explain in greater detail how he arrived at $k_D$? For example, why did he discard the limit as ${R \to 0}$? Why is only ${R \to \infty}$ used in the final formula? Why was he able to extract everything but $\frac{1}{\dot\tau}$ from the integral (since R is also a function of $\eta$)?

While function $f(\eta)=\frac{1}{6(1+R(\eta))}\left( \frac {16}{15}+ \frac{R(\eta)^2}{(1+R(\eta))}\right)$ is relatively constant, it does change with $\eta$ and looks like this:

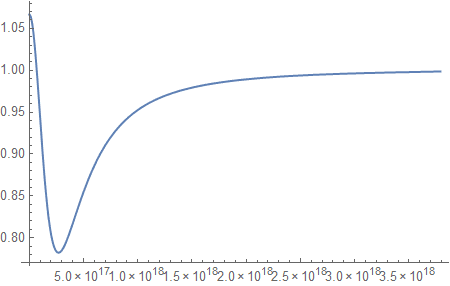
and the function $g(\eta)=\frac{1}{\dot\tau(\eta)}$ looks like this:

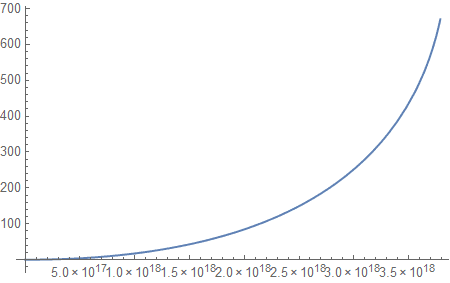
The bottom axis is $\eta$.

 

[mitochan]

Hello.
I would like to know more information to elaborate. Integral in your post means integral over the region [-infinity, +infinity] or any other ?

 

[Quarkly]

Hello.
I would like to know more information to elaborate. Integral in your post means integral over the region [-infinity, +infinity] or any other ?

There are several sources for this equation. Some write it as an indefinite integral, others write it as $$k_D^{-2}(\eta)=\int_0^{\eta} \frac{1}{6(1+R)}\left( \frac {16}{15}+ \frac{R^2}{(1+R)}\right)\frac{1}{\dot\tau} d\eta$$I believe this is the more rigorous form. Both R and $\dot\tau$ are functions of $\eta$. I believe the author of these notes may have been trying to solve the integral in parts as $R[0]$ and $\dot\tau[0]$ are undefined.

 

[mitochan]

Thanks for your explanation.

I would like to confirm my understanding on your graphs.

--As R is relative baryon-photon momentum ratio,
f(0)=1/6 * 16/15 where R=0 no baryon existed and f(+infinity)= 1/6 where R=+infinity all photon momentum will be reduced to zero by expansion of universe.
Your first graph read f(0)=1.066 and f(+infinity)=1 so it seems graph of 6f with coefficient 6 multiplied.

-- Is unit of base $\eta$ axis second? If so around 5 E+17 points on the graph is where we are.

 

[Quarkly]

--As R is relative baryon-photon momentum ratio,
f(0)=1/6 * 16/15 where R=0 no baryon existed and f(+infinity)= 1/6 where R=+infinity all photon momentum will be reduced to zero by expansion of universe.
Your first graph read f(0)=1.066 and f(+infinity)=1 so it seems graph of 6f with coefficient 6 multiplied.

-- Is unit of base $\eta$ axis second? If so around 5 E+17 points on the graph is where we are.

Many apologies. You are correct. The graph for $f(\eta)=\frac{1}{6(1+R(\eta))}\left( \frac {16}{15}+ \frac{R(\eta)^2}{(1+R(\eta))}\right)$ looks like this (I forgot the factor of 1/6 in the original plot):

Not sure what you're asking in the second question. The bottom axis is conformal time and the units are seconds. And, yes, $3.5 \times 10^{18} s$ is $\eta_0$, the present time (according to the model).

Also, the form is correct, but the units were wrong on the optical depth plot. Here are the correct units in km. (though, this should be immaterial for the answer).

 

[mitochan]

Thanks for your clarification.

With assumption and observation that

--The author refers value of $\eta$ around $\eta_0$, the age of universe for us,
13.8 billion year = 4.35 E+17 second,

--The second graph curve in the region $\eta [0,\eta_0]$ read g($\eta$) be small positive constant (not zero, I expect) , and

--due to decline in the first graph curve in the region $[0,\eta_0]$ integral coefficient seems a little bit less (or more?) than 1/6 but the difference is negligible in our approximation,

I think the integral would become 1/6 $g(\eta)\eta$. I do not think this relation hold for any value of $\eta$, much more than $\eta_0$, for an example.

 

[Quarkly]

Your answer is little more than an opinion. I was looking for a derivation likely involving integration by parts, but something that took me step-by-step from the first equation to the authors analytical solution (or a disproof, if the author was wrong).