How would you classify this Excitation Force?

[henlus]

Hi guys, I will really appreciate it if you respond to this my question.

Actually I am working on a linear generator that can be use on land to generate electricity from the movement of vehicles.

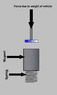
The system consists of a magnet that is connected to a spring as shown in the picture. The magnet is surrounded by a coil of wire which is not shown in the diagram. The system will be constructed in such a way that when a vehicle move over it, a plunger will slide down a cylinder and push down the magnet against the spring force. Once the vehicle have pass, the plunger will be forced upward to its original position above the magnet, leaving the magnet to oscillate.

Now the question is this: How would you classify the excitation force in this system? I know it is not a sinusoidal force. I have been suspecting it to be a rectangular pulse. I will be happy to get your views.

 

[Eynstone]

Is the mutual magnetic induction of the coil & the magnet to be taken into account? We can construct a simple model based on that.

 

[henlus]

Yes the mutual induction of the coil and magnet will be taken into account. All the ebooks i have come across have always used two equations to predict power output and these equations are the mechanical and electrical equations. I will appreciate any input to this question but my main problem is identifying the type of excitation force the system will experience.

 

[Eynstone]

Would you share the differential equations set up? We could solve explicitely for the force.

 

[henlus]

Thanks for your reply Eynstone, here is the differential equations:

my"+cy'+ky=F(t) ……..mechanical equation

where m=mass of the magnet
c=damping coefficient
k=spring constant
y=displacement of the magnet
y’=velocity of the magnet
y’’=acceleration of the magnet

Bly'=Lq"+(Ri+RL)q' ……………..electrical equation

Where B= magnetic flux density of the magnet
l= active length of the coil
q’= current in the coil (i.e time rate of change of charge, q)
Ri= resistance of the coil
RL= resistance of the inductor

The problem is the F(t) and how to solve for it.