- #1
Violagirl
- 114
- 0
Homework Statement
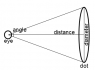
A) Under optimum conditions, the smallest black dot that can be seen subtends an angle of 2.3 x 10-6 rad. If a dot is viewed at a distant of 0.25 m, the near point of a normal adult, what is the smallest diameter it can have and still be seen? B) The maximum resolution is obtained when the image falls on the fovea centralis. At 10° away from this region, the acuity is 10 times poorer. What is the minimum size spot that can be seen at that angle under these conditions?
Homework Equations
Pf = 1/xf + 1/D
Pf = person's far point, 1/xf = distance a person sees an object, D = image distance
Pn = 1/xn + 1/D
Pn person's near point, 1/xn - distance a person sees an object, D = image distance
A = Pn - Pf
A = power of accommodation
sin θ = 1.22 (λ/d)-power of acuity equation
λ = wavelength, d = diameter
The Attempt at a Solution
I've puzzled over this problem. I'm not sure what the relevant equation would be unless I'm missing one. Any help is appreciated.