I have to work out Fault MVA and draw impedance diagrams

[David J]

Homework Statement

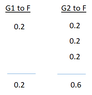
For the system shown in FIGURE 2, using a 10 MVA base, calculate the fault MVA levels through each unit and the base "voltage" MVA across each unit for a fault at F. Draw the impedance diagrams showing the fault levels and the base "voltage" MVA across each unit for:

(a) bus section switch B open and A open

(b) bus section switch B closed and A open.

Other circuit breakers are closed.

The generators have the same rating and characteristics.

Figure 2 is shown in the attached PDF

Homework Equations

shown in the attached PDF

The Attempt at a Solution

My attempt is 4 pages long and so I have not been able to create in Latex form so I have attached the question and my answer in PDF. I am hoping someone can take a look at this and advise if its ok or if there any areas I have made a mistake etc[/B]

 

[magoo]

When you converted the transformer impedance in per unit on 10 MVA, I think you made a mistake. If you convert the per unit impedance to ohms and then put it in per unit on the larger MVA base, you'll see that the per unit value will be smaller, not larger, than 0.1.

 

[David J]

Do you mean in the first section of my answer?
I used the equation as per the lessons I have been given.
The bus couplers at this stage of the answer are both open so I am assuming each transformer impedance to be 0.2 p.u.
Later on in the question when the bus coupler B is closed then this value does reduce to 0.1 because the two transformers are operating in parallel.
Can you identify the part of the answer you are referring to please?
thanks

 

[magoo]

Right in the beginning (page 1), where you say "I need to convert the transformer to 10 MVA"

Starting with the procedure that I outlined, convert the transformer % or pu impedance to ohms. Then, your system base is 10 MVA.

The base impedance will be given by the ratio of the transformer impedance (in ohms) divided by your base impedance.

The result is not 0.2!

 

[magoo]

My apologies. I made a mistake and now agree with your 0.2 pu value for the transformer impedance on the 10 MVA base.

 

[David J]

Its ok, so what about the rest of the answer? I think page 2 is ok but unsure about pages 3 and 4

 

[magoo]

For part a, the fault is between G1 and its associated transformer T1.

G1 feeds the fault at its terminals. Its MVA rating is 10 and its impedance is 0.2. There is no source on the load side of T1, so it doesn't supply any fault current.

G2 and T2 are isolated from the fault because of the open switches. No fault current from G2 and T2.

Do you understand this?

 

[David J]

Yes, I fully understand this and I have explained this in page 2 of my answer. I would expect the fault level at point F (shown on the first page) to be in the region of 50MVA. ( $\frac{10 MVA}{0.2}=50 MVA$) If the fault was on the other bus bar then I would expect this value to be in the region of 25 MVA ($\frac{10 MVA}{0.2+0.2}=25 MVA$)
I do understand the fact that the RHS is totally out with this question whilst the bus couplers are open. I work in this industry and I am senior authorized for HV switching of this nature but sadly we don't often get involved in actual design stuff like this

 

[magoo]

What you just said is correct, but what you have on your page 2 says the fault level through the G1/T1 leg is 25 MVA and also 25 MVA for the G2/T2 leg. The 25 MVA values only apply when the fault is on the lower bus, but the problem has it on the upper bus.

I'm confused.

 

[David J]

Ok this makes sense to me. In my page 2 I have called it the "total Fault level"
The question is asking me to calculate the fault MVA levels through each unit and the base voltage MVA levels across each unit "for a fault at F". I have calculated for a fault on the lower bus. I need to change that. It should read: -

the fault level through the G1/T1 leg for a fault at F using a 10MVA base will be$\frac{10}{.2}=50 MVA$

I don't need to mention the G2/T2 leg as it has nothing to do with the fault at F as long as the bus couplers are open.
The two diagrams I have created on page 2 are not really necessary either. I think the first diagram is all that is required. The second drawing refers to a fault on the lower bus which is not asked for in the question.
Moving onto page 3 I have tried to identify the voltage MVA base for all units instead of just for a fault at F. Can you confirm I have calculated the voltage MVA base correctly. I think the 5 MVA values are correct in this case

 

[magoo]

Your use of the term "voltage MVA base" is confusing. The MVA base is set by the problem, namely 10. I', not sure what you mean here.

The diagram you show on page 3 is for case a, but without a fault.

Your diagram for part b on the top of page 4 is not quite correct. The way I redrew it, the generators and transformers are not it parallel.

I put an X to indicate the fault. So G1 feeds the fault only limited by its own impedance. G2 feeds the fault but includes T1 and T2 impedances in addition to its own.

So mine is not in parallel.

 

[David J]

I have attached an example from one of my lessons and this is what I am working to for information to help me answer my question

My question asks me to calculate the base "voltage" MVA across each unit for a fault at F. I think I may have made the same mistake here as I did earlier when working out the fault MVA but this is where I am asking advice. Hopefully the attached exerts from one of the lessons will help explain where I am coming from and what I am trying to do.

For my solution on page 3 I have taken the fault MVA as $\frac{10 MVA}{0.2+0.2} = 25 MVA$ This is where I went wrong before but continuing on I then needed to proportion the MVA to each unit so for the generator G1 I get $25*0.2 = 5 MVA$ and again for the transformer T1 I get $25*0.2=5 MVA$

Regarding the running of the generators with Bus Coupler A open and Bus Coupler B closed the generators must be synchronized to do this, surely ?? To have 2 generators feeding to series loads like this then to close the bus coupler further down the line would require a check sync relay before the breaker would be allowed to close so the system must surely be in parallel when either the A bus coupler or B bus coupler is closed

 

[magoo]

That base "voltage" MVA is something I was not familiar with, so I appreciate your attaching it. I think I understand it now.

For part b, I am going to trace out the path to the fault from G2 since it is more involved. The path from G1 to F simply involves a pu impedance of 0.2. The path from G2 involves G2, T2 and T1 as shown below.

Here are the pu impedance for each path:

The resulting short circuit MVA is the base MVA divided by the pu impedance, or

So there is a total short circuit MVA of 66.7.

Now, to apply what I learned from your attachment, base "voltage" MVA for the path from G1 is simply 10 MVA across a 0.2 pu impedance.

For the path from G2 to the fault, the resulting 10 MVA will have 3 equal parts, each 0.33 pu.To your discussion, I agree you would have to have one generator picking up the entire load and then have to synchronize the other one before closing it in.

I hope some of this helps.

 

[David J]

Hello again. This has helped yes. There were a few issues with my answer which were incorrect. I understand this now so I will mark this as solved. Thanks again for the help