ethanmuncher
- 3
- 0
[SOLVED] i think this should be simple, but i need help!
this isn't really homework, but I'm having trouble figuring this problem out...
the problem says:
In this diagram, the red part has an area of 800 square centimetres.
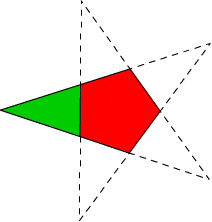
What is the area of the green part, in square centimetres? Please round up to the nearest whole number.
i have no idea how to solve this, since the only information they give is that the pentagon is 800 square centimeters...
Well, I figured out that you could probably fold the green triangle into the pentagon, and make it 3 triangles, the 2 on the sides being congruent... but how do i figure out an area?
Homework Statement
this isn't really homework, but I'm having trouble figuring this problem out...
the problem says:
In this diagram, the red part has an area of 800 square centimetres.
What is the area of the green part, in square centimetres? Please round up to the nearest whole number.
Homework Equations
i have no idea how to solve this, since the only information they give is that the pentagon is 800 square centimeters...
The Attempt at a Solution
Well, I figured out that you could probably fold the green triangle into the pentagon, and make it 3 triangles, the 2 on the sides being congruent... but how do i figure out an area?