Ideal monatomic gas engine problem

[ken12380]

Homework Statement

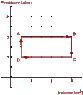
An ideal monatomic gas is confined to a cylindrical container having a movable, yet "snuggly-fitting," lid that slides up and down to accommodate changes in pressure and volume. The diagram shown below, outlines the steps in a heat cycle starting at position A and moving through positions B, C, D and then back to A.

*ignore the axes labels*
PV diagram2
Given:
PA = PB = 12.0 atm
PC = PD = 6.0 atm
VA = VD = 5.0 m3
VB = VC = 30.0 m3
temperature of point C is 900 K
moles of gas are present 2437.3376

How much total heat is added during the cycle?

Homework Equations

Q=nCp delta T
Q=nCv delta T
PV=nRT

The Attempt at a Solution

I tried:
Q=Q+Q=nCp delta T+nCv delta T=2437.3376*20.78*150+2437.3376*12.47*1500
=53187581 J but this is wrong.
Why? and what is the actual answer?

 

[Andrew Mason]

You have to determine where heat is being added. It is being added(flowing into the gas) when the gas pressure increases at constant volume and when the gas expands at constant pressure. Heat flows out when it loses pressure at constant volume and when it is being compressed at constant pressure. You have to calculate only the heat flow INTO the gas.

AM