Exploring If Space Was Quantised: Travel Paths & Bird Paths

[qbit]

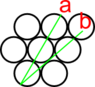
I recently moved to a city where the streets are arranged in a grid: they run East-West or North- South. To visit a friend South-East of my location, I can, say, head South on the street I'm on for 3 blocks and then turn East onto the street She lives on for 3 blocks. If I had traveled 1 unit of distance South and 1 unit East, the total distance I traveled would be 2 units. If there were streets running in diagonally in the South-East / North-West direction, I need have traveled only 2^0.5 units.
Had I gone East from my starting point and turned South at the corner of the first block, then East at the end of that block, then South, then East and finally South, I would have arrived at my friend's location and covered a distance of 2 units.
I have tried to include a couple of diagrams to illustrate.
Now, I hope you'll agree that no matter how many times each block is subdivided with more East-West and North-South streets, I will always have to travel 2 units to my friend's location. This journey I'll refer to later as the 'travel path'.
In the absence of diagonal streets and access to an aerial vehicle, only birds can take the more direct journey of 2^0.5 units. This journey I'll refer to later as the 'bird path'.

So, now to my question. If 3 dimensional space was quantised, consisted of very small bits packed together and could not be traversed in an omnidirectional fashion but were more like houses with a limited number of entries and exits, what shape would they need to be such that bird path is 1 unit to any location from my starting location AND is always x units to that same location should I travel there? In other words, a radial distance of x 'in' space and a radial distance of 1 'out' of space (where x > 1)?

I imagine that if the travel path was 1 unit and the bird path was 1 unit to any location from a given starting point, then the spatial tessellation of quantised space would have to permit omnidirectional travel. But if the travel path was always greater than the bird path and that travel path was the same in every direction as was the bird path, what kind of tessellation is required? A semi chaotic one?

If it turned out that the travel path did vary with direction as compared to the bird path, how would one go about measuring this, assuming that difference was not too small to measure?

I realize there are some big 'ifs' in this question, so any thoughts as to why it's not worth exploring are very welcome. Thanks for your response in advance.

 

[Haelfix]

This is an old line of thought and a paradox that goes back to the Greeks. Later popularized by Hermann Weyl.

If each atom or lattice of space is say 1 unit long, you run into a problem with recovering the pythagorean rule of the continuum world. No matter how small you make the lattice spacing, and how far away you look, such a discrete world is flagrantly in violation of observation.

This is called the 'Weyl tile' paradox, feel free to google it.

 

[marcus]

...
So, now to my question. If 3 dimensional space was quantised, consisted of very small bits packed together ...

Your assumption is unrelated to modern quantum gravity approaches. Approaches for example like Loop or Spinfoam do not have "space" consisting of very small bits packed together.

So your question is irrelevant to QG, although it stands on its own as an abstract math thought experiment.

 

[qbit]

Thanks Haelfix and marcus.

Haelfix, I had not heard of a Weyl tile. Thanks for that info. I guess I stumbled onto this problem but realized that square tiles are not workable in 2D land and cubes in 3D world equally so. What I was interested in knowing is what shape should these unit volumes be such that there is no “problem with recovering the pythagorean rule of the continuum world” as you said.

marcus, I was of the understanding that it is the popular belief amongst physicists that space was divided up into small, indivisible unit volumes or quanta. Both for Loop Quantum Gravity and String Theory. But they work in many more dimensions than the problem I posed and so, as you say, is unrelated to modern quantum gravity approaches.

I imagine that if the material world is divided into 'atoms' that the spatial world must be as well or there is no chance of a unified theory. How to reconcile discrete on an continuum? Besides, I'd always thought that infinity (including infinitely small divisions) is a useful concept to model phenomena that can be measured with Very Large Numbers, but in itself is not real.

 

[atyy]

Your assumption is unrelated to modern quantum gravity approaches. Approaches for example like Loop or Spinfoam do not have "space" consisting of very small bits packed together.

What about section 6.10 in Rovelli's http://relativity.livingreviews.org/Articles/lrr-2008-5/ ?

 

[marcus]

Thanks for pointing out. There are variants that do have fundamental discreteness. Section 6.10 is about those. They are offshoots, not the mainstream version. But they exist!

 

[marcus]

marcus, I was of the understanding that it is the popular belief amongst physicists that space was divided up into small, indivisible unit volumes or quanta.

Qbit, I never heard of such a belief being popular (or even at all common) among physicists.

It's not the normal or usual assumption in Loop Quantum Gravity.
BTW Loop doesn't use extra dimensions.

There is an approach to quantum gravity---which like Loop is 4D, it doesn't use extra dimensions---which approximates spacetime geometry using a huge number of equal size blocks. but it doesn't say that space or spacetime is MADE of actual blocks. They go right ahead and refine the approximation by replacing the blocks with smaller ones. They don't treat the blocks as indivisible. It is just a mathematical method.
that approach is called Triangulations and my sig has a link to a SciAm article about it by Renate Loll. It is one of the easiest to understand approaches to QG.

Loop does not use a bunch of equal size blocks. Triangulations does, as an approx. But does not assume space is made of them.
Both theories do not focus on space, or on spacetime. They focus on geometry, and geometrical measurement. The theories are not concerned "what space itself is made of".

The substantive issues involve the measurement of geometric quantitities at different scales by differerent observers. How these change over time. How they are affected by matter.

As a rule quantum theories tend to be concerned with measurement. So it is not surprising that quantum geometry (gravity = geometry) should be concerned with geometric measurement.

I'm a bit tired (it's bed time) and may not be making sense to you. Perhaps tomorrow I'll have time to improve this.

 

[qbit]

Thanks again, Marcus. Your descriptions are excellent. I'll investigate further.

I looked up Planck Length. I'm embarrassed to say that for the longest time I believed it to be a unit of space that was indivisible. So now I'm scratching my head as to what a continuous space means. I thought Zeno's logic was pretty good.

 

[marcus]

Good to see you--best wishes for your talk at the conference!

Well your intuition might be correct. We don't know. All I am doing is reporting the main currents in nonstring QG and QC (the application to cosmology.) At present there are elements of discreteness in some quantum operators that represent taking some geometric measurements.

I'm talking about the man-made theory. It has some aspects of discreteness, which are interesting and get a lot of research attention. But it hasn't yet gone whole-hog into discreteness where the whole shebang is made up of little morsels of spacetime. That could come in time though! I sort of hope it doesn't.

An "operator" in this jargon is a mathematical machine that extracts numbers from quantum states of the world ("wavefunctions" members of a giant menu of quantum states or conditions of the world called a "Hilbertspace").

If you give the operator a sample wavefunction, it will chew it up and spit out a number. That corresponds to somebody taking a measurment in some realworld lab.

An operator might for example correspond to a guy measuring the area of a certain slit that an electron is trying to go thru. Even though the underlying world is continuous, the operator might for some reason only have a discrete set of area numbers that it is willing to spit out. The list of possible outcomes of a measurement operator is called its "spectrum". There is a lot of jargon that goes back in history to when quantum mechanics was first formulated and even earlier.

To make it more confusing, some perfectly good nonstring QG approaches have measurement operators which do NOT have a discrete spectrum. Like Renate Loll's Triangulations QG. But the approach that is currently getting the most attention which is Loop/Spinfoam QG does have some discrete spectrum operators.

Its confusing but people are getting on with it doing the best they can, and the theories keep changing and evolving. So it is hopeful and interesting too---not a total bummer.

 

[qbit]

Marcus, much of what you've written sounds distantly familiar (10+ years ago) when I was a chemist. I've tried to keep up with developments over those years but I fear I've forgotten more than I've learnt. One thing that seems to have stood out in that time, is something I think I can use an analogy to explain.
This is highly speculative and simplistic, but I get the feeling that the fundamental structure of the universe is generally considered to be like a train wheel on a rail. The train wheel is discrete matter: indivisible because an infinitely small wheel just won't work as a wheel. The rail is spacetime. The wheel can be located on any point on the rail because it is continuous (I'm leaving out uncertainty, here). I'll probably have to pester the number theorists, but it's my intuition that this is not a good way to view the universe if a cogent unified theory is ever to be synthesised.
My reasoning goes like this: spacetime may truly be continuous, but for humans to measure and hence comprehend it, a discrete model may be the key. Our present comprehension of information is discrete: realized in the manifestation of the computer. Again, I should state that this idea is highly speculative and most likely, highly contentious. The more I think about discrete spacetime, the more problems I encounter. It has nasty implications for such things as basic as 'direction'.
I've tried to attach a drawing to help illustrate one of the problems.
The two green lines represent the paths taken by two particles, 'a' and 'b' through quantised 2D space represented by black circles packed together. As you can see, there is 'space' in between the circles. Particle b is shown to move through this 'in between' space. I could explain this away by saying that particle b 'tunnels' through this in between space such that it only really exists in the 'circle' space. But then the particle will have traveled farther than its equal, a, that does not pass through this in between space. This is not our experience.
Alternatively, I could have a discrete matter particle that is vastly larger than the discrete spatial circles such that they're spread out over a considerable number of them. This, I think, solves the direction and distance problem and might not be incongruous with position / momentum uncertainty. But the problem with this is that I doubt this really explains any kind of phenomena at all. Or for that matter, predict any new phenomena that can be measured. Besides, I'm sure someone vastly more knowledgeable than myself has played with this idea and found it lacking to say the least.
I guess I'm posting this in the hope that someone, perhaps you, might get some modicum of inspiration to do something really interesting with physics. I bought Lee Smolin's, The Trouble With Physics and I'm about to read it with a sense of trepidation.