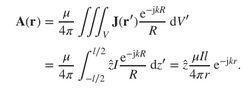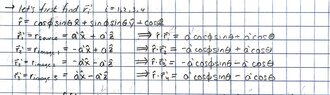Image Theory for an Electric Dipole

[stateissuedrx78]

Homework Statement

A short vertical electric dipole of moment Iℓ (pointed in z direction) is placed at (a,0,a) [the xz plane, y-axis is in and out of page] and there are two infinitely long PECs, one located on the x-axis and one located at the z-axis. Use image theory to remove the two PEC planes and replace their effects with properly positioned and oriented three additional image dipoles. Calculate the vector 𝑵(𝜃,𝜙) due to the four dipoles (source + three images).

Relevant Equations

attached inline.

PREFACE: My first real post so please bear with me and my notation and layout. I tried to make it as easy on the eyes as possible...

While I am fairly confident of my process thus far, I feel I may be straying from the answer a bit towards the end.

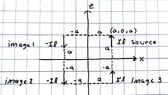
Considering the short vertical electric dipole in the +z direction, the images should be the following (I have also attached my own drawing):
source: located at (a,0,a) - oriented in the +z direction with moment Iℓ
image 1: located at (-a,0,a) - oriented in the -z direction i.e. -Iℓ moment (tangential components of E should be zero across the PEC plane)
image 2: located at (-a,0,-a) - oriented in the -z direction i.e. -Iℓ moment (normal component of E should reinforce image 1)
image 3: located at (a,0,-a) - oriented in the +z direction i.e. +Iℓ moment (normal component of E over PEC should reinforce the source)

Now, for vector N(𝜃,𝜙):
- In the textbook I am using, I found that the magnetic vector potential of an infinitesimal dipole (taken from "short" dipole as stated in the question) oriented the exact same is as given below:

The textbook also states that N and A have the following relationship

with N(𝜃,𝜙) given as

where r'cosΨ = r_hat*r'. where r_hat is just the r unit vector in cartesian form and r' is the source/image distance vector.
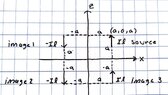
My logic is that N(𝜃,𝜙) for the source dipole would simply be Iℓ*exp(jkr_hat*r') in which the total N(𝜃,𝜙) would just be
N(𝜃,𝜙) = N(𝜃,𝜙)_source+N(𝜃,𝜙)_image1+N(𝜃,𝜙)_image2+N(𝜃,𝜙)_image3
or more explicitly as written below (sorry for the sloppy writing):

My next thought was to simply integrate these N's over the surface element dS=dxdz (or dx'dz' to be pedantic). I have not passed this point as the integration seems a bit brutal to tackle without some possible advise on the work so far. Thanks in advance!

 

[berkeman]

My first real post so please bare bear with me

LOL, fixed that for you.

 

[WWGD]

LOL, fixed that for you.

 

[TSny]

Hello and welcome to PF!

I'm not sure of the interpretation of the problem statement. Is the dipole oscillating harmonically with some angular frequency $\omega$? So, $k = \dfrac \omega c$?

What does PEC stand for? (Maybe "perfect electrical conductor"?)

Also, it appears to me that you are assuming $a \ll r$.

You have an answer for $\vec N$:

My logic is that N(𝜃,𝜙) for the source dipole would simply be Iℓ*exp(jkr_hat*r') in which the total N(𝜃,𝜙) would just be
N(𝜃,𝜙) = N(𝜃,𝜙)_source+N(𝜃,𝜙)_image1+N(𝜃,𝜙)_image2+N(𝜃,𝜙)_image3
or more explicitly as written below (sorry for the sloppy writing):

It looks to me that this is probably correct. (I wouldn't put primes on the $a$'s.) You can simplify the sum $N_s + N_1 + N_2 + N_3$ to a fairly simple expression.

My next thought was to simply integrate these N's over the surface element dS=dxdz (or dx'dz' to be pedantic). I have not passed this point as the integration seems a bit brutal to tackle without some possible advise on the work so far. T

I don't understand why you want to integrate N over the x-z plane, or what that would even mean.
The question only asks for an expression for $\mathbf{N}(\theta, \phi)$, which you have.

 

[WWGD]

View attachment 358145

Bear(s) with me.

 

[kuruman]

He's exercising his constitutional right to bare arms.

 

[PhDeezNutz]

The image configuration you have looks right to me (I’ve done a similar problem before).

Forgive my ignorance but why are we calculating a vector potential for electric dipoles?

 

[TSny]

The image configuration you have looks right to me (I’ve done a similar problem before).

Forgive my ignorance but why are we calculating a vector potential for electric dipoles?

I was a little confused about that also. But, if the electric dipole is oscillating, we can calculate A(r) for the radiation field.

 

[PhDeezNutz]

I was a little confused about that also. But, if the electric dipole is oscillating, we can calculate A(r) for the radiation field.

That is fair. Hopefully OP will clarify.

 

[stateissuedrx78]

Hello and welcome to PF!

I'm not sure of the interpretation of the problem statement. Is the dipole oscillating harmonically with some angular frequency $\omega$? So, $k = \dfrac \omega c$?

What does PEC stand for? (Maybe "perfect electrical conductor"?)

Also, it appears to me that you are assuming $a \ll r$.

You have an answer for $\vec N$:



It looks to me that this is probably correct. (I wouldn't put primes on the $a$'s.) You can simplify the sum $N_s + N_1 + N_2 + N_3$ to a fairly simple expression.


I don't understand why you want to integrate N over the x-z plane, or what that would even mean.
The question only asks for an expression for $\mathbf{N}(\theta, \phi)$, which you have.

- in the problem it is not mentioned if it is oscillating
- my apologies, yes PEC = perfect electrical conductor
- the end goal of the problem, which perhaps was dumb of me to leave out, is to find E and H in the far-field region and the vector N is related to the far field E via

where we can ignore L in this instance.
BUT as you've brought it to question, i see now that i do not need to integrate over any surface for N because I have replaced the integral procedure with the initial logic of using the relationship between the magnetic vector potential A and the vector N (as the integration is built into A, if that makes sense??)

 

[stateissuedrx78]

That is fair. Hopefully OP will clarify.

the problem does not state if it is oscillating BUT i am using a previous result found in the same book (Theory and Computation of Electromagnetic Fields - Jian Ming Jin) for an infinitesimal electric dipole's magnetic vector potential (i am assuming this is also infinitesimal judging by the problem's word choice of "short") which I then used its relationship to N to find said vector if that makes sense. let me know if i'm not being clear enough. I appreciate everyone's input thus far!

 

[stateissuedrx78]

View attachment 358145

View attachment 358145

the animal or the man

 

[PhDeezNutz]

With the exponential phase factor $e^{jkr}$ I’m inclined to think this system has to be oscillating and therefore radiating.

The reason that there’s no time dependence in the expression for $\vec{E}$ is because the expression for $\vec{E}$ is the average field.

It’s been awhile so I could be wrong.

 

[stateissuedrx78]

With the exponential phase factor $e^{jkr}$ I’m inclined to think this system has to be oscillating and therefore radiating.

The reason that there’s no time dependence in the expression for $\vec{E}$ is because the expression for $\vec{E}$ is the average field.

It’s been awhile so I could be wrong.

I'm inclined to agree about the exponential factor. I believe it may just be an innate detail given by the problem/material at hand that just isn't explicitly said.

 

[stateissuedrx78]

just wanted to follow up and say that i was correct in my setup. thanks everyone!