Imaginary factor in WAVE guide TE field

[FrankJ777]

Hey guys. I'm trying to comprehend the TE_mn EM fields in wave guides. I've gone through the derivation, using Pozar's microwave textbook, and for the most part it's straight forward. I am having a hard time though determining what the effect of the imaginary factor in the field equations are.
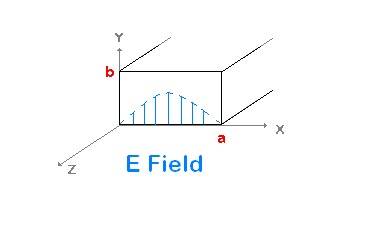
Here is the simplest case, a TE₁₀ wave propagating in the z direction, with a picture of the waveguide dimentions and the E field as I would imagine it to be.
The E and H fields are given as:

E$_{y}$ = $\frac{-jωμm\pi}{k^{2}a}$ A sin$\frac{mx\pi}{a}$ e$^{-jβz}$

H$_{x}$ = $\frac{jβm\pi}{k^{2}a}$ A sin$\frac{mx\pi}{a}$ e$^{-jβz}$

I understand there is a dependency on z from the e$^{-jβz}$ factor.
I also understand there is a time and frequency dependancy (not shown) from e$^{jωt}$ factor.
But what I'm really trying to understand is, how does the factor, $\frac{-jωμm\pi}{k^{2}a}$ , effect the fields?
I'm not sure how I should tread the imaginary factor in this case.
Thanks a lot.

 

[the_emi_guy]

When we use complex numbers to describe real quantities, such as amplitudes of fields along a waveguide, the real value is found by multiplying by e^jωt then taking the real part.

Ey(x,y,z,t) = $Re[\frac{-jωμm\pi}{k^{2}a}$ A sin$\frac{mx\pi}{a}$ e$^{-jβz}$e$^{jωt}]$:

These steps are not written explicitly but are understood.

 

[FrankJ777]

Thanks emi guy, but I think you missunderstood what part I was asking about. I got that there is an assumed factor e$^{jωt}$, but what I didn't understand was the first factor, colored red, in the Ey field equation below.

Ey(x,y,z,t) = Re $[\frac{-jωμm\pi}{k^{2}a}$ A sin$\frac{mx\pi}{a}$ e$^{-jβz}$e$^{jωt}]$:

I've been thinking about it though, about what it's affect on the E field is. If you could tell me if I'm right or not I'd be grateful.
Using the identity: j = e$^{j\frac{\pi}{2}}$

The Ey field becomes:
Ey(x,y,z,t) = Re $[\frac{ωμm\pi}{k^{2}a}$ A sin$\frac{mx\pi}{a}$ e$^{-jβz}$e$^{jωt}$ e$^{-j\frac{\pi}{2}}$ ]

which is
$[\frac{ωμm\pi}{k^{2}a}$ A sin$\frac{mx\pi}{a}$ cos($\omega$t - βz - 90°)

which will just delay the phase 90° as the wave propagates along the z direction.

Hope I'm on the right track. Thanks!