Impact velocity after exiting circular motion

Join the discussion
Registration is free. Ask a follow-up in this thread, or start your own.
Sign up Log in
5 replies · 1K views
dogge76
Messages
3
Reaction score
0
Hello,

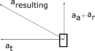
i want to determine the velocity with which an object moves after it has departed a rotating disk. In my problem there is a disk rotating with the angular speed w. On this disk there is a drilling in which a mass m is positioned. In case the thread in the drilling fails i need to determine the velocity with which this mass hits the housing. During the rotation there is a force F_a additionally to the centrifugal force. My idea is to determine the tangential velocity with v_t=rw and with F=ma i can determine the acceleration due to the force F_a. Do i need to determine another accelerations or velocities. I am doing a rough calculation therefore the calculation doesn't need to consider all possible effects. I inserted a scetch of the problem. I would very welcome some help. thanks
 

Attachments

  • kreis.png
    kreis.png
    12.9 KB · Views: 482
Physics news on Phys.org
@dogge76 Welcome to this forum, sorry for weird response above. I don't have time to look carefully at the problem now, but I'm sure someone will. (Maybe next time post it in the "homework" section using the template offered there.)
 
Last edited by a moderator:
dogge76 said:
During the rotation there is a force F_a additionally to the centrifugal force.
Does F_a still act after the mass is released? If not, then the mass will hit the housing with the tangential speed it had on release (ignoring air resistance etc.). What might be relevant for the damage to the housing is the impact angle, which depends on the radii of disc and housing.
 
@Krylov thanks for the welcome. I don't mind what the other guy said. I don't have time for such folly.

@A.T. No F_a doesn't really act after the mass is released but i think it does partially. This force comes from an oil pressure which means that some force will still act after release. The impact angle isn't very interesting at this point. But i don't really understand why it will only hit with the tangential speed, what about the force F_a ? In the very first moment it will surely accelerate the mass , wouldn't it ? And doesn't the centrigual force contribute to some radial acceleration ? i have added a scetch. a_a means the acceleration due to the Force F_a . a_r comes from the rotation.
 

Attachments

  • beschleunigung.png
    beschleunigung.png
    7.7 KB · Views: 461
dogge76 said:
No F_a doesn't really act after the mass is released but i think it does partially.
You have to make up your mind here.

dogge76 said:
And doesn't the centrigual force contribute to some radial acceleration ?.
If you analyse it from the inertial frame, there is no centrifugal force.
 
No F_a won't act after the mass is released