Implementing a function in simulink simulation

[Evo8]

Homework Statement

The problem statement essentially has me inputing a signal into simulink manipulating it and then looking at the output.

My output function is defined as $$y(n)=0.8x(n)+0.5x(n-1)+0.2x(n-2)$$

Homework Equations

N/A

The Attempt at a Solution

In my simulink canvas I have placed a sine wave as my source and a scope as the sink or output.

To implement this function i tried the block called discrete filter. I have connected them in series respectively.

When I open the parameters for the filter i have fields for numerator and denominator coefficients. So I took my Y(n) and calculated the z transform then found my H(z).

y(n)=0.8x(n)+0.5z^{-1}x(n)+0.2z^{-2}x(n)
y(n)=x(n)(0.8+0.5z^{-1}+0.2z^{-2})
H(z)=0.8+0.5z^{-1}+0.2z^{-2}

So i put the coefficents into my filter parameters.
Numerator was [0.8 0.5 0.2]
Denominator was [1]

My input sine wave was left at the default of 1amplitude and 1 rad/sec.

My input and parameters:

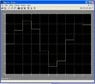
This is what my output looks like.

Am I on the right track here? I am not really sure what my expected outcome should be.

Thanks for any help.

 

[I like Serena]

Let's see...

So you have a sine input and a filter that does $y(n)=0.8x(n)+0.5x(n-1)+0.2x(n-2)$.
The filter would take 3 consecutive values of the sine input and replace it by a weighted average.
What kind of output would you expect in such a case?
Can you say anything about the amplitude (since it's a weighted average)?

 

[Evo8]

I guess I don't really understand how the weighted average would apply.

So the three consecutive values I assume are 0.8, 0.5 and 0.2? With 0.2 having the least weight? I would suspect that the amplitude would be decreased in certain areas. I am thinking that may not be the case since my output waveform had amplitudes that exceed 1? Of course I am not sure if that filter was implemented properly.

 

[I like Serena]

Suppose you have 3 consecutive values that are all close to the top of the sine, which is 1.
What would the value of the filter be?

Similarly, suppose you have 3 consecutive values that are all close to 0.
What would the value of the filter be?

Finally, suppose you have 3 consecutive values close to the valley of the sine at value -1.
What would the value of the filter be?

 

[Evo8]

Im not sure that I completely follow.

3 consecutive values close to the top of the filter (1) I would guess the value of the filter to be close to 3?

For the values close to 0 i would guess it would be close to 0

For the values close to -1 following the same convention I would guess -3?

 

[I like Serena]

You have the filter y(n)=0.8x(n)+0.5x(n-1)+0.2x(n-2).

Suppose x(n)=x(n-1)=x(n-2)=1, what would y(n) be?
It would not be 3.

 

[Evo8]

Well I would be left with just the coefficients right? So y(n)=1.5

 

[I like Serena]

Exactly. :)
The same would happen when the sine is around -1.

The resulting output would look like a sine, just like the input, with an amplitude that is more than 1, but less than 1.5.

Does your output graph look like that?

 

[Evo8]

It certainly does! Its a bit blocky but that must be my sampling frequency in the simulation. I will have to play with it.

Thanks again for all of your help Ilse. Much appreciated!

 

[I like Serena]

Have fun playing!