Induction & Energy: Rod Moving Down Inclined Surface in Uniform Magnetic Field

[hokhani]

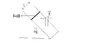
suppose a rod of mass m and resistance R,is going down the inclined surface in the uniform magnetic field( see figure).
in the steady state the velosity of rod will be constant. if we use the work-kinetic energy theorem,
W= delta K
deltak=0(kinetic energy is constant)
you know W is pertaining to gravity force and magnetic force
and i think W also include dissipation energy in wire namely (i^2)R(deltat)
from this point of view i can't get the correct response for the stady state velocity of rod
(it is double of the correct answer)?!

 

[zorro]

How is there a force 'ILB' when there is no current through the rod?

 

[hokhani]

MR ABDUL QADEER:
there is an inducted current.
please guide me
thanks

 

[zorro]

there is an inducted current.

Not unless you connect a conducting wire across the rod. If it simply moves on the surface there will be an induced E.M.F. but no current.

 

[hokhani]

exuse me
I forgot to say:
it forms a circuit
please guide me now

 

[zorro]

Ok.
If you analyse the external forces acting on the rod during its motion with constant velocity, you will find that the work done by these forces is equal in magnitude but opposite in sign. So they cancel each other giving change in K.E. of rod = 0, which is in accordance with Work-Energy theorem. One can also say that the power dissipated in the resistor equals that due to weight when the velocity of the rod becomes constant.