Martin Harris
- 102
- 6
- Homework Statement
- Induction Motor calculation
- Relevant Equations
- $$Psn (stator nominal power) = Pelectrical (electrical input power)$$
$$Psn (stator nominal power) = \frac {Pn} {efficiency}$$
$$sn(nominal slip) = \frac {Ljr} {Pelectromagnetic} $$
$$ Ωn (nominal speed) = Ωs * (1-sn)$$
$$Mn(nominal torque) = \frac {Pn} {Ωn}$$
$$ILs (stator line current) = \frac {Psn} {sqrt(3) * uls * cosφ}$$
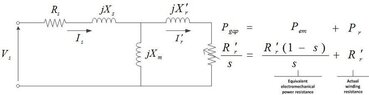
Given the AC Induction (asynchronous motor) in 3 phases:
Requirements:
a) Power loss calculation, Power loss balance.
b) sn (nominal slip) = ? Ωn (Nominal speed) = ? Mn (nominal torque) = ?
c) ILs (current through the statoric line) = ?
Attempt at a solution:
a) LFe= Lmechanical = $$ \frac {1.5} {100} * 5000 W = 75 W$$
Hence, LFe = Lmechanical = 75W (Iron loss = Mechanical loss = 75W)
Lv = $$ \frac {1} {100} * 5000 W = 50 W$$
Hence Lv = 50W (ventilation loss on the rotor)Psn (stator nominal power) = Pelectrical (electrical input power) = $$\frac {Pn} {0.9} = 5555.5555555555555555555555555556 W$$
i) $$ Ljs + Ljr = Psn - (Pn+Lfe + Lmechanical +Lv) = 5555.555555555555556 W - 5200W$$
$$ Ljs + Ljr = 355.5555555555555555555555555556W $$
ii) $$Ljr = \frac {2} {3} * Ljs$$
from i) and ii)
$$Ljs = 213.33333333333333333333333333336 W $$
$$Ljr = 142.22222222222222222222222222224 W $$
$$ Pelectromagnetic (electromagnetic power) = Psn(input electrical power) - Ljs - LFe $$
$$ Pelectromagnetic= 5555.55555555555555556 W - 213.33333333333333333333336 W - 75W $$
$$ Pelectromagnetic = 5267.2222222222222222222222222222 W$$
$$Ltotal (totalloss) = Ljs+LFe+Ljr+Lmechanical+Lv = 555.5555555555555555556 W$$
$$Ltotal (totalloss) = 555.5555555555555555555555555556 W$$
b) $$sn(nominal slip) = \frac {Ljr} {Pelectromagnetic}$$
$$sn= \frac {142.22222222222222222222222222224 W} {5267.2222222222222222222222222222 W } $$
$$sn(nominal slip) = 0.02700137116337939035966670182471 [-] $$
$$ Ωn (nominal speed) = Ωs * (1-sn)$$
where Ωs is the (synchronization speed)
$$Ωs = \frac {2*π*fstator} {p} = \frac {2*π*50Hz} {2} =157.07963267948966192313216916398 [rad/s] $$
$$Ωn (nominal speed) = 157.079632679489661923132 [rad/s] * (1-0.027001371163379390359)$$
$$Ωn = 152.838267215303462845785704096[rad/s]$$
$$ns (syncrhonization speed) [rpm] = \frac {60*fstator} {2} = 1500 [rpm]$$
$$nn (nominal speed) [rpm] = ns*(1-sn) = 1500 [rpm] * (1-0.02700137116337939035966670)$$
$$nn (nominal speed) [rpm] = 1459.4979432549309144604999472629 [rpm] $$
$$Mn(nominal torque) = \frac {Pn} {Ωn} = \frac {5000W} {152.83826721530346284578570409637 [rad/s]}$$
$$Mn(nominal torque) = 32.714320118249532323572617030565 [Nm] $$
c) $$Psn (electrical power input) = sqrt(3) * uls * ILs * cosφ$$
Hence
The current through the stator line:
$$ILs = \frac {Psn} {sqrt(3) * uls * cosφ} = \frac {5555.5555555555555555555555555556 W} {sqrt(3) * 220V * 0.88}$$
$$ILs = 16.567673013935541910845637640667 [A]$$
I would be more than grateful if someone can confirm these calculations.
Many thanks!
| Parameter | Value |
| Pn (Nominal Power) = Pmechanical (output power at the shaft) | 5 kW = 5000W |
| uls (Voltage through the stator line) | 220 V |
| fstator (stator frequency) | 50 Hz |
| p (Number of pole pairs) | 2 |
| LFe (Iron loss) = Lmechanical (mechanical loss) | LFe = Lmechanical 1.5% Pn |
| Lv (Ventilation loss on the rotor) | Lv = 1%*Pn |
| LJr (Rotor Joule loss) = (2/3) * LJs (Stator Joule loss) | #To be calculated below# |
| η (efficiency of the induction motor) | 0.9 |
| cosφ (power factor) | 0.88 |
Requirements:
a) Power loss calculation, Power loss balance.
b) sn (nominal slip) = ? Ωn (Nominal speed) = ? Mn (nominal torque) = ?
c) ILs (current through the statoric line) = ?
Attempt at a solution:
a) LFe= Lmechanical = $$ \frac {1.5} {100} * 5000 W = 75 W$$
Hence, LFe = Lmechanical = 75W (Iron loss = Mechanical loss = 75W)
Lv = $$ \frac {1} {100} * 5000 W = 50 W$$
Hence Lv = 50W (ventilation loss on the rotor)Psn (stator nominal power) = Pelectrical (electrical input power) = $$\frac {Pn} {0.9} = 5555.5555555555555555555555555556 W$$
i) $$ Ljs + Ljr = Psn - (Pn+Lfe + Lmechanical +Lv) = 5555.555555555555556 W - 5200W$$
$$ Ljs + Ljr = 355.5555555555555555555555555556W $$
ii) $$Ljr = \frac {2} {3} * Ljs$$
from i) and ii)
$$Ljs = 213.33333333333333333333333333336 W $$
$$Ljr = 142.22222222222222222222222222224 W $$
$$ Pelectromagnetic (electromagnetic power) = Psn(input electrical power) - Ljs - LFe $$
$$ Pelectromagnetic= 5555.55555555555555556 W - 213.33333333333333333333336 W - 75W $$
$$ Pelectromagnetic = 5267.2222222222222222222222222222 W$$
$$Ltotal (totalloss) = Ljs+LFe+Ljr+Lmechanical+Lv = 555.5555555555555555556 W$$
$$Ltotal (totalloss) = 555.5555555555555555555555555556 W$$
b) $$sn(nominal slip) = \frac {Ljr} {Pelectromagnetic}$$
$$sn= \frac {142.22222222222222222222222222224 W} {5267.2222222222222222222222222222 W } $$
$$sn(nominal slip) = 0.02700137116337939035966670182471 [-] $$
$$ Ωn (nominal speed) = Ωs * (1-sn)$$
where Ωs is the (synchronization speed)
$$Ωs = \frac {2*π*fstator} {p} = \frac {2*π*50Hz} {2} =157.07963267948966192313216916398 [rad/s] $$
$$Ωn (nominal speed) = 157.079632679489661923132 [rad/s] * (1-0.027001371163379390359)$$
$$Ωn = 152.838267215303462845785704096[rad/s]$$
$$ns (syncrhonization speed) [rpm] = \frac {60*fstator} {2} = 1500 [rpm]$$
$$nn (nominal speed) [rpm] = ns*(1-sn) = 1500 [rpm] * (1-0.02700137116337939035966670)$$
$$nn (nominal speed) [rpm] = 1459.4979432549309144604999472629 [rpm] $$
$$Mn(nominal torque) = \frac {Pn} {Ωn} = \frac {5000W} {152.83826721530346284578570409637 [rad/s]}$$
$$Mn(nominal torque) = 32.714320118249532323572617030565 [Nm] $$
c) $$Psn (electrical power input) = sqrt(3) * uls * ILs * cosφ$$
Hence
The current through the stator line:
$$ILs = \frac {Psn} {sqrt(3) * uls * cosφ} = \frac {5555.5555555555555555555555555556 W} {sqrt(3) * 220V * 0.88}$$
$$ILs = 16.567673013935541910845637640667 [A]$$
I would be more than grateful if someone can confirm these calculations.
Many thanks!
Last edited: