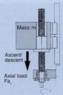
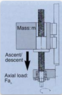
Inertial force acceleration (vertical axis)

[Justin71]

Hi,

How is the inertial force Fi (acceleration) when the system is vertical. I noted Fi_horizontal=m.a, Ff=mg.μ.cos(Θ) et Fg=mg.sin(Θ) .

 

[jackwhirl]

How is the inertial force Fi (acceleration) when the system is vertical.

Hi, Justin. Could you rephrase that question a little? It's not clear to me what you are asking.

 

[Justin71]

I would like know the difference between the inertial force when our system is in vertical position (like on right) and the inertial force when our system is in horizontal position (like on left). Because I know with the horizontal positon, we have Fi=m.a but with the vertical position ? Does a coefficient count ? Thanks

 

[jackwhirl]

F=ma regardless of orientation. The acceleration, a, and the force, F, are vectors. They have both magnitude and direction. Changing the direction of the force will change the direction of acceleration, but not the governing equation.

Does that answer your question?

 

[Justin71]

We don't need an angle ? For me, the acceleration load isn't the same according to vertical position of the load (on right) and horizontal position (on left).
For this formula,

For Fi, whathever vertical or horizontal, it is the same formula (a position angle does not count in the calculation?).

So, if we are on the vertical position,

Fa= Fm + Fg + Fa where Fg=mg.sin(Θ) and Fa=m.a. Is just that ?

 

[jackwhirl]

Fa= Fm + Fg + Fa where Fg=mg.sin(Θ) and Fa=m.a. Is just that ?

Let's back up a bit, because I don't understand what you're asking.
Can you define a few terms?
What is Fa? From context, it looks like the total force input required to perform the machine operation.
What is 'the acceleration load'?

I assume the following:
Fm, the Machining Force, is the ideal force required to execute the machine operation.
Ff, the Frictional Force, is the force of friction, resisting any operation.
Fi, the Inertial Force, is the force required to overcome the inertia of the moving parts at a given acceleration.
Fg, the Gravitational Force, is the portion of the weight of the machine that works for or against the operation.

 

[CWatters]

We don't need an angle?

If it's vertical you know the angle and the net force is just m(a+g).

 

[Justin71]

Excuse me jackwhirl I was a little bit confused :

So I correct, I would like to define the total force of the system during ascents and descents of the load

I have Fa=Fm+Fg+Fi+Ff with Ff=0.

I wanted to ask you if Fi=m.a (like in horizontal position) despite the vertical position of the system. I so, then Fa = Fm+ mg.sin(Θ) + m.a ?

To understand what I want, I would like define the required torque to the motor for lift the load lift the load with the formula : T=(Fa x screw_lead)/(2*pi*efficiency)

 

[jackwhirl]

Yes, Fi = m*a independent of orientation.
Remember that gravity will be working with you on the descent and against you on the ascent, and be careful to get your signs right.

 

[Justin71]

Ok thank's ! I found 2 picture on the net without explication and I don't understand the result :

and it's write :

I have the terms highlighted in orange but others I do not understand in particular :