Infinite wires with current, magnetic field vector

[scholio]

Homework Statement

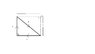
three infinitely long straight wires are arranged in a plane as shown at the left. what is the magnetic field vector at point A(see attach.)? all wires carry current I

Homework Equations

F = IL X B where x indicates cross product, I is current, L is length, B is magnetic field

magnetic field, biot-savart law, B = mu_0/4pi[integral(IdL/r^2)] where mu_0 is constant = 4pi*10^-7, dL is change in length, r is radius/distance, I is current

The Attempt at a Solution

not too sure about how to start, this is what i am thinking of:

first, determine the net magnetic field at the center of the triangle formed by the three wires, and then use the distance from the center of that triangle to point a, as value r in the biot-savart equation.

i have a feeling that since the problem asks for a vector, i need to analyze each wire individually based on their direction, is this a correct assumption?

help appreciated

 

[dynamicsolo]

The wires actually follow the sides and diagonal of a square, which means we can take advantage of some symmetry for this (though not in an obvious way).

What you'll need to derive is the expression for the magnetic field at a point at a perpendicular distance r from the midpoint of a current-carrying wire segment of length L. You use Biot-Savart and the integration is symmetrical around the midpoint of the wire.

You would then use your result for three fields:

1) for the wire on the "vertical" side of the square, you use half your result for a point at a distance a from a segment of length a ;

2) for the "horizontal" side of the square, you use the same value as in (1) above ; and

3) for the diagonal, use the full field value for a point
a/sqrt(2) away from a wire of length a·sqrt(2), but with the field direction pointing the other way. (Use the right-hand rule for the three segments to see why the parts add this way.)

If the magnetic field for a wire segment is already derived in your book, you can just use it; otherwise, the integration isn't too bad...