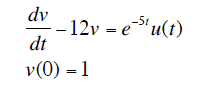SUMMARY
The discussion focuses on solving an initial value ordinary differential equation (ODE) using the Laplace Transform. The equation presented is sV(s) - V(0) - 12V(s) = U(s+5), leading to V(s) = [U(s+5) + 1] / (s - 12). Participants clarify the application of the shifting property in Laplace Transforms, specifically how to transform U(s+5)/(s-12) and the Laplace Transform of e^(at) * u(t), where u(t) represents the Heaviside step function.
PREREQUISITES
- Understanding of Laplace Transforms
- Familiarity with ordinary differential equations (ODEs)
- Knowledge of the Heaviside step function
- Ability to apply shifting properties in Laplace Transforms
NEXT STEPS
- Study the properties of the Laplace Transform, focusing on the shifting property
- Learn how to apply the Inverse Laplace Transform to various functions
- Explore the application of the Heaviside step function in differential equations
- Investigate the Laplace Transform of exponential functions multiplied by step functions
USEFUL FOR
Mathematicians, engineers, and students studying differential equations, particularly those interested in the application of Laplace Transforms in solving initial value problems.