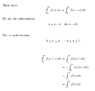Speedking96
- 104
- 0
Homework Statement
This is the problem with the solution:
Can someone please explain how the new bounds were computed, I don't quite understand what's going on with the inequalities?
Also, in the final two steps, how can the f(u) change to f(x)?