MHB Integral of Logarithm: Find & Solve

[alyafey22]

Find the following integral :

$$\int^{\infty}_{0} \frac{\ln(x) }{x^2+a^2}\,dx$$

 

[Prove It]

Find the following integral :

$$\int^{\infty}_{0} \frac{\ln(x) }{x^2+a^2}\,dx$$ <----- THERE IT IS!

Hope that helped :)

 

[TheBigBadBen]

Find the following integral :

$$\int^{\infty}_{0} \frac{\ln(x) }{x^2+a^2}\,dx$$

I am sure that there's some nice little trick to all this, but here I go anyway...

u-substition:
$$
u = \ln(x);\; du = dx/x \rightarrow\\
\int^{\infty}_{0} \frac{\ln(x) }{x^2+a^2}\,dx=
\int^{\infty}_{-\infty} \frac{u}{e^{2u}+a^2}\,e^u du\\
=\int^{\infty}_{-\infty} \frac{u}{e^{u}+a^2e^{-u}}\, du
$$

Well, that's my stab at it for now. More on that when I'm less sleepy.

 

[chisigma]

Find the following integral :

$$\int^{\infty}_{0} \frac{\ln(x) }{x^2+a^2}\,dx$$

Setting $\frac{x}{a}= t$ the integral becomes...

$$I= \frac{\ln a}{a}\ \int_{0}^{\infty} \frac{d t}{1 + t^{2}}\ dt + \frac{1}{a} \int_{0}^{\infty} \frac{\ln t}{1+ t^{2}}\ dt = \frac{\pi}{2}\ \frac{\ln a}{a} + \frac{1}{a} (\int_{0}^{1} \frac{\ln t}{1+ t^{2}}\ dt + \int_{1}^{\infty} \frac{\ln t}{1+ t^{2}}\ dt)\ (1)$$

... and setting in the last integral in (1) $\xi= \frac{1}{t}$ we obtain...

$$I= \frac{\pi}{2}\ \frac{\ln a}{a} + \frac{1}{a}\ (\int_{0}^{1} \frac{\ln t}{1+ t^{2}}\ dt - \int_{0}^{1} \frac{\ln \xi}{1+ \xi^{2}}\ d \xi) = \frac{\pi}{2}\ \frac{\ln a}{a}\ (2)$$

Kind regards

$\chi$ $\sigma$

 

[alyafey22]

$$F(b) = \int^{\infty}_0 \frac{x^b}{x^2+a^2}\, \, $$ ----(1)

$$F(b) = \frac{1}{a^2}\,\int^{\infty}_0 \frac{x^b}{\frac{x^2}{a^2}+1} \, dx$$

Let $$\frac{x^2}{a^2} = t$$

$$F(b) = \frac{a^b}{2|a|} \,\int^{\infty}_0 \frac{t^{\frac{b-1}{2}}}{t+1} \, dt = \frac{a^b \, \pi }{2|a| \sin\left( \pi \frac{b+1}{2}\right)}$$

$$F(b)=\frac{a^b \, \pi }{2|a| \sin\left( \pi \frac{b+1}{2}\right)}$$

Differentiate wrt to $b$

$$F'(b) = \frac{a^b \, \pi \, \ln|a| }{2|a| \sin\left( \pi \frac{b+1}{2}\right)} - \frac{a^b \, \pi^2 }{4|a| } \cot^2 \left(\pi \frac{b+1}{2}\right)$$

$$F'(0) = \frac{ \, \pi \, \ln|a| }{2|a|} $$

Differentiating (1) wrt to $$b$$ we get :

$$F(b) = \int^{\infty}_0 \frac{x^b \ln(x) }{x^2+a^2} \, dx$$

$$F'(0) = \int^{\infty}_0 \frac{\ln(x) }{x^2+a^2} \, dx\, \, $$ ----(2)

By (1) , (2) we get what we want $$\square$$ .

 

[alyafey22]

There is a complex analysis approach , if someone is interested . I will try to post it later .

 

[alyafey22]

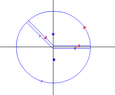
Here is a complex approach

$$f(z) = \frac{\log_0^2(z)}{z^2+a^2}$$

Where the logarithm has a branch cut on the positive real axis and the integration is along a circle with radius $$R$$.

We will divide the contour into two parts because the function is not analytic in the whole contour , so we can't apply the residue theory directly. We can easily prove that the sum of the integration along the two parts will eventually be $$2\pi i \, \text{Res}(f(z))$$ . The sum of integration along the two tilted lines will be equal to $0$.

View attachment 923

The picture shows two separated parts while there should be no distance between the two contours . So the two lines should be on the x-axis but I moved them a little bit for easy illustration and to identify direction .
Integration along the x-axis

$$\int^R_0 \frac{\ln^2(x)}{x^2+a^2}\, dx$$Integration along the x-axis ( opposite direction )

$$-\int^R_0 \frac{(\ln(x)+2\pi i)^2}{x^2+a^2}\, dx=-\int^R_0 \frac{\ln^2(x)+4\pi i \ln(x)-4\pi^2}{x^2+a^2}\, dx$$Integration along the Circle

$$\int_{C_R}\frac{\log_0 ^2(z)}{z^2+a^2}\, dz \leq 2 \pi R \frac{\ln^2|R|+ 2\pi \ln|R| +4\pi^2}{R^2-a^2} \to 0 \,\,\,, R \to \infty$$Sum of Residues Here we are assuming that $$a>0$$ to easily find the residues $$\text{Res}(f(z) ; ai) +\text{Res}(f(z) ; -ai) =\frac{\log_0^2(ai)}{2ai}-\frac{\log_0^2(-ai)}{2ai} $$$$\frac{\left(\ln(a)+\frac{\pi}{2}i \right)^2}{2ai}-\frac{\left(\ln(a)+\frac{3\pi}{2}i \right)^2}{2ai}= \frac{-2 \pi \ln(a)i +2\pi^2}{2ai}$$Now take $$R\to \infty$$ and sum the contours

$$-4\pi\text{P.V} \int^{\infty}_0 \frac{ \ln(x)}{x^2+a^2} \, dx -4\pi^2 \text{P.V} \int^{\infty}_0 \frac{dx}{x^2+a^2}\, dx = 2\pi i\left( \frac{-2 \pi \ln(a)i +2\pi^2}{2ai}\right)$$Comparing the imaginary parts


$$-4\pi\text{P.V} \int^{\infty}_0 \frac{ \ln(x)}{x^2+a^2} \, dx= -\frac{2 \pi ^2 \ln (a)}{a}$$$$\text{P.V}\int^{\infty}_0 \frac{ \ln(x)}{x^2+a^2}\, dx = \frac{\pi \ln (a)}{2a} \,\,\, a>0$$We also get by comparing the real part $$ 4\pi^2 \text{P.V} \int^{\infty}_0 \frac{dx}{x^2+a^2} = \frac{2\pi^3}{a}$$

$$\int^{\infty}_0 \frac{dx}{x^2+a^2} = \frac{\pi}{2a}$$