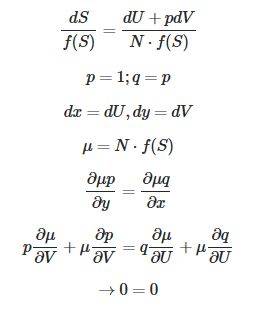B4cklfip
- 18
- 0
- Homework Statement
- Show that if N is an integrating factor also N*f(S) is an integrating factor.
- Relevant Equations
- ##dS = \frac{dU+pdV}{N}##
I'm not sure if that is the right way to solve this excersice. Can someone maybe help and tell me if this calculation proofs the statement ?