- #1
franco1991
- 20
- 0
Two coherent waveforms (could be pulses or wavetrains), that intersect at an angle, as in the picture below.
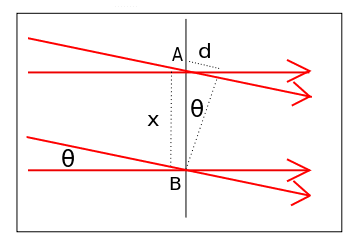
Assume that we are able to make the waveforms in phase and superposed at the point of intersection, such that they constructively interfere.
In what direction does the resultant wave propagate? Both waves, though superposed, are traveling in different directions. Does the resultant wave travel in one of the two component (original) waveforms' directions, or does it propagate forward at a 90 degree angle from the point of intersection, such that the resultant wave is traveling in a slightly different direction that either of the original waveforms (forward from the point at which they were superposed)?
Assume that we are able to make the waveforms in phase and superposed at the point of intersection, such that they constructively interfere.
In what direction does the resultant wave propagate? Both waves, though superposed, are traveling in different directions. Does the resultant wave travel in one of the two component (original) waveforms' directions, or does it propagate forward at a 90 degree angle from the point of intersection, such that the resultant wave is traveling in a slightly different direction that either of the original waveforms (forward from the point at which they were superposed)?