Intermediate-Calculate a weight using conservation of energy

[Aleoa]

Homework Statement

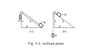
This problem comes from the Feynman Lectures. However, the author doesn't explain in detail the procedure to solve the problem.
I have to calculate the weight W using only the law of energy conservation.

Homework Equations

In the second picture W it is lowered of 5 units.
The known weight block is 1 lb.

How can I solve this problem and why ?
In order to apply conservation of energy do I have to assume some properties of this system we are studying?
Thank so much

 

[CWatters]

Hint: The string is a fixed length but if the height of one mass changes the height of the other mass doesn't change by the same amount due to the slope.

 

[Aleoa]

If i apply some force on W and i let it down for 5 units of length (like the pictures), the same force is applyed to the 1 lb block, so the net energy cancels out. However, since the displacement of 5 units of length of W generated the same energy (in absolute value) of 3 units of length of 1 lb ---> W = 3/5 lb.

It's okay or it's possible to do better ? Feynman asks to solve with using only the conservation of energy law...

 

[CWatters]

What's the equation for the change in PE?

 

[Aleoa]

How it's possible to change the configuration of the blocks without violating the conservation of energy law ?

Why if i apply a force on the block W, that makes it go down, I'm SURE that the net energy is balanced by a amount of negative energy produced by the 1 lb block, so that the total energy is 0 ?

 

[CWatters]

How it's possible to change the configuration of the blocks without violating the conservation of energy law ?

The problem statement does not mention friction. So there are no losses that have to be overcome.

Why if i apply a force on the block W, that makes it go down, I'm SURE that the net energy is balanced by a amount of negative energy produced by the 1 lb block, so that the total energy is 0 ?

Correct.

The problem statement tells you to use this fact (conservation of energy).

 

[CWatters]

Write an equation for the change in PE and sum it to zero... Eg...

Change in PE of W + Change in PE of 1kg = 0

Solve for W.

 

[Aleoa]

Write an equation for the change in PE and sum it to zero... Eg...

Change in PE of W + Change in PE of 1kg = 0

Solve for W.

If i solve the equation you correctly suggest, i will obtain W = 3/5 lb.

My question is a little more subtle. If we are in a real case ( and we consider the lever as reversible, even if in reality isn't possible) and i want to go from the configuration 1 (where W is up) to configuration 2 (where W is down), i have to exert some energy in the system.
Why this transitory is neglected and we consider only the two configurations, and not the transitory that allowed to go from configuration 1 to configuration 2 ?

 

[CWatters]

My question is a little more subtle. If we are in a real case ( and we consider the lever as reversible, even if in reality isn't possible) and i want to go from the configuration 1 (where W is up) to configuration 2 (where W is down), i have to exert some energy in the system.
Why this transitory is neglected and we consider only the two configurations, and not the transitory that allowed to go from configuration 1 to configuration 2 ?

Let us break it down into steps...

Assumptions:

The string has zero mass
m = total mass of both W and 1lb.
There is no friction

Steps:

1) Configuration 1 - system is stationary
2) You apply a force that accelerates the system to some velocity V (eg the system gains KE=0.5mv^2).
3) The system moves at constant velocity V. (Mass W looses some PE, 1lb mass gains some PE, KE is constant)
4) You apply a force that decelerates the system from V down to zero (eg The system looses KE=0.5mv^2)
5) Configuration 2 - system is stationary

So the KE gained in step 2) is the same as that lost in 4). So we do not need to consider it.

 

[CWatters]

If there is friction F_f then to move the weights additional energy is required. How you account for this depends on how the initial force is applied.

One way is to apply a small additional force, let's call it F₊ constantly to counteract friction. In other words F₊ and F_f are equal and opposite. That way the weights don't slow down in step 3.

If d is the distance moved then...

Without friction...

ΔKE + ΔPE = 0

with friction

ΔKE + ΔPE + F₊*d + F_f*d= 0

Remember that F₊ and F_f act in opposite directions.