Internal energy in the context of rest energy

[etotheipi]

I've come across some conflicting definitions and hoped someone more in-the-know could clarify a few points.

The rest energy is the total energy of the system in its rest frame; I read about the following (approximate!) semi-empirical mass formula earlier, and if we multiplied this through by $c^{2}$ we'd end up with the total rest energy of the nucleus equalling the sum of the inherent energy of the actual protons and neutrons, $c^{2}[(A-Z)m_{n} + Zm_{p}]$, added to the other terms (which are all defined on Wikipedia, including contributions from the strong force etc.).

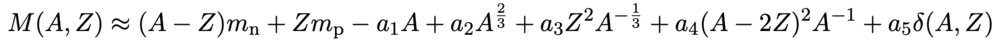
I'm wondering how the internal energy is defined generally (assuming it even is) in relation to the rest energy. In thermodynamics, it seems like it's taken to be the sum of kinetic energies relative to the COM and internal potential energies. However, this doesn't include the inherent mass-energies of the actual particles in your system, which led me to believe that the rest energy includes the internal energy.

I'm probably being naïve here, but how far off would I be in claiming that we could say the rest energy equals the sum of the internal energy and the mass-energies of the individual particles? In the context of the SEMF, I would be claiming that the first two terms can be considered the inherent mass-energy ($/c^{2}$) and the final five can be grouped into "internal energy" ($/c^{2}$). In this case, we'd always have $\Delta E_{rest} = \Delta U$, which on a side-note also seems to fit nicely with the work-energy principle for non-rigid bodies.

Please do let me know if I'm sort of going in the right direction or if I'm still a few parsecs off...

 

[vanhees71]

In modern physics the thermodynamic potentials are defined in the (local) restframe of the medium. That leads to the most simple generalizations of the thermodynamic quantities from Newtonian to relativistic physics, i.e., entropy, temperature, and chemical potentials are all scalar (fields). Also usually one includes the rest energies in the energy balance, because then energy and momentum build a four-vector.

Unfortunately, even the issue with "relativistic mass" has not been taken over by all modern textbooks, though it was clear that it is a unnecessary confusion, and the more convenient notion of invariant mass is known since about 1907/1908 (with Minkowski's reanalysis of special relativity in terms of spacetime geometry). Now you can imagine, how even more confusing old-fashioned ideas about the relativistic generalization of the thermodynamic quantities persist to be discussed even in the newer literature since the modern view has been established only in the late 1960ies. A very illuminating paper about this is

https://doi.org/10.1103/PhysRev.173.295

There he clarifies the issue by first reviewing the different notions by the founding fathers (Planck's vs. Ott's version) and than giving the modern manifestly covariant description, and only this latter one is really free of confusion (as only the notion of invariant mass is free of confusion in comparison to ideas about various kinds of "relativistic masses").

 

[etotheipi]

A very illuminating paper about this is
https://doi.org/10.1103/PhysRev.173.295

Unfortunately I don't have access to this, though it sounds interesting; is there anything similar that is freely available?

 

[DrStupid]

I'm wondering how the internal energy is defined generally (assuming it even is) in relation to the rest energy.

The internal energy of a system is defined as its total energy excluding the kinetic energy of the whole system and its potential energy in external fields.

 

[etotheipi]

The internal energy of a system is defined as its total energy excluding the kinetic energy of the whole system and its potential energy in external fields.

In that case, is it identical to the rest energy? The bit I don't understand is that if we take, for instance, an ideal gas with $N$ molecules, the internal energy is $U = \frac{3}{2}NkT$ however this doesn't take into account the mass-energies of any of the molecules themselves. Maybe it's because that particular equation is not relativistic?

 

[DrStupid]

In that case, is it identical to the rest energy?

Yes, it is pretty much the same.

The bit I don't understand is that if we take, for instance, an ideal gas with $N$ molecules, the internal energy is $U = \frac{3}{2}NkT$ however this doesn't take into account the mass-energies of any of the molecules themselves.

The full equation would be $U = U_0 + \frac{3}{2}NkT$. But as long as $U_0$ remains constant, it can be omitted from the calculation. Usually you finally get a difference between two states and all constant terms cancel out in such a difference.

Maybe it's because that particular equation is not relativistic?

Yes, in special relativity it would be possible to set $U_0 = m \cdot c^2$ (even though it is not usefull in the equation above). But in classical mechanics $U_0$ is unknown in general. It might have any value between $-\infty$ and $+\infty$ and cannot be determined by experiments or in theory. Therefore it makes even less sense to include it into the calculation.

 

[etotheipi]

@DrStupid Ah, so essentially whenever the absolute value internal energy is included in an equation, we should just treat it as the difference between the actual total internal energy and the rest energies of the individual constituent particles ($U_{0}$ as you put it)!

 

[DrStupid]

Ah, so essentially whenever the absolute value internal energy is included in an equation, we should just treat it as the difference between the actual total internal energy and the rest energies of the individual constituent particles ($U_{0}$ as you put it)!

Not only the rest energies of the individual constituent particles but all parts of the internal energy that are not relevant for the calculation (e.g. the potential energy due to the gravitational interaction between the particles).

 

[Chestermiller]

Not only the rest energies of the individual constituent particles but all parts of the internal energy that are not relevant for the calculation (e.g. the potential energy due to the gravitational interaction between the particles).

In thermodynamics, the absolute internal energy is virtually never needed, and the internal is virtually always specified relative to some well-defined reference state.