Intersection coordinates in lattice

[aaaa202]

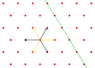
On the drawing below is a hexagonal lattice. For the basis vectors one can choose either the set of arrows in black or the set in yellow. The intersection coordinates of the plane in green seems to be the same regardless of choosing the black or the yellow basis. Why is that? My teacher said it is due to the 6-fold symmetry of the lattice while for me it seems like sheer accident.
I know of course that a hexagonal lattice has 6-fold symmetry, which for me means that I can rotate it by 60 degrees about any point and it will look the same. But how do I translate this symmetry property into a rotation of 60 degress of the basis vectors?
I know this question might be obvious to you, but I am having a hard time exactly seeing how to apply symmetry properties. How do YOU intuitively see it?

 

[haruspex]

I'm not entirely sure I understand the question. It would help if you were to post the expressions you have for the co-ordinates and indicate the sense in which they are the same in both bases. But assuming I'm interpreting correctly:
Instead of rotations, consider another symmetry.

 

[aaaa202]

What otter symmetries deles the lattice have? Should I mirror it in an axis? In this case which?

 

[haruspex]

What otter symmetries deles the lattice have? Should I mirror it in an axis? In this case which?

Yes, I'm thinking of a reflection. What sort of reflection leaves the line unchanged?

 

[aaaa202]

In an axis perpendicular to the line. So reflection in that axis will transform from one basis to the other and the lattice is the same. But does that tell me that the choosing one basis or the other gives the same? I feel like I am still missing the crucial point.

 

[haruspex]

In an axis perpendicular to the line. So reflection in that axis will transform from one basis to the other and the lattice is the same. But does that tell me that the choosing one basis or the other gives the same? I feel like I am still missing the crucial point.

You have to ask yourself what you mean by the coordinates being the same.
Since you will be using different basis vectors, you must mean not that they are automatically the same but that they can be made to look the same by a suitable mapping between the bases. Moreover, it need not be that each individual point on the green line gets the same coordinates, so you also need to find a mapping of the line to itself.
Having understood that, I think it's fairly easy to see from the diagram that this can be done.