Trav44
- 4
- 0
Homework Statement
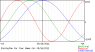
Hi guys I was wondering how to find the points of intersections between 3 different sine graphs.
For an assignment I am trying to find when my three biorhythms (Physical, Emotional, Intellectual) will all cross at once.
Each cycle runs on the following time frame:
Physical Cycle - 23 days
Emotional Cycle - 28 days
Intellectual Cycle - 33 days
Homework Equations
I have converted the three into equations
Physical
A=100 for 100%
B=
T=2pi/B which can be re-arranged to B=2pi/T
B=2pi/23
B=0.2732
C=N/A
D=N/A
y=100sin0.2732x
Emotional
A=100 for 100%
B=
T=2pi/B which can be re-arranged to B=2pi/T
B=2pi/28
B=0.2244
C=N/A
D=N/A
y=100sin0.2244x
Intellectual
A=100 for 100%
B=
T=2pi/B which can be re-arranged to B=2pi/T
B=2pi/33
B=0.1904
C=N/A
D=N/A
y=100sin0.1904x
Am I calculating the equation for each of these graphs correctly?
How do I find when all of the graphs will equal the same x-value at one time?
The Attempt at a Solution
I have no idea where I would start? Is there an equation for this? or do i put a certain number as the x-value for each graph? Find factors of the periods multiplied together? Something else?
Any help will be much appreciated thank you :)