Introduction to Theory of Quintics

[mathbalarka]

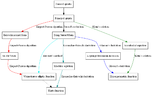
This is a graph containing the main Tschirnhausen transformations of a general quintic and the algorithms to solve them. The methods would be explicitly described most probably elsewhere in this forum

https://www.physicsforums.com/attachments/1786._xfImport

• The lower-most nodes are the elementariest functions to which the root of a general quintic can be extracted.
• In any sub-graph of the above, the lowermost elements are the form reduced from the topmost elements via Tschirnhausen transformations.
• Deeper colors indicates the effectiveness of the algorithm in computational research, as well as popularity.
• Dotted lines indicates a reduction that is non-obvious although not a part of the interest, in most cases.
• Black lines indicates a transformation that is not part of the algorithm.
• The red arrows indicate the Kiepert algorithm, which I like to call Kiepert-Perron algorithm.
• The green arrows indicate Glasser's derivation.
• The magenta-like colors indicate Hasner's method and Kronecker-Brioschi derivation respectively.

Any comment/question regarding this thread should be posted in http://mathhelpboards.com/commentary-threads-53/commentary-introduction-theory-quintics-8210.html

 

[mathbalarka]

This is a commentary thread for "http://mathhelpboards.com/math-notes-49/introduction-theory-quintics-8208.html"

Any comments/question pertaining to the tutorial should be posted here instead of the tutorial thread.

 

[DreamWeaver]

Superb thread, Balarka! :D

On the bottom RHS of the schematic you posted, what's the order of the "hypergeometric functions" mentioned? I'm assuming 3F2 rather than 2F1, but might well be wrong, hence my asking...

Thanks! (Hug)

Gethin

 

[mathbalarka]

On the bottom RHS of the schematic you posted, what's the order of the "hypergeometric functions" mentioned?

That'd be $_4F_3$. In general, Glasser's method gives you $_6F_5$, but a two fold reduction to $_4F_3$ is possible.

 

[DreamWeaver]

That'd be $_4F_3$. In general, Glasser's method gives you $_6F_5$, but a two fold reduction to $_4F_3$ is possible.

Thanks, Balarka! (Handshake)

I missed this one at the time, but just came across the following paper by M.L. Glasser yesterday...

403 Forbidden